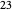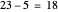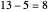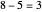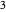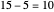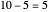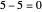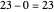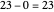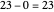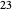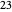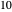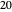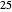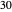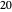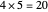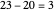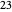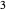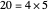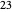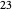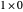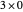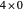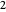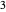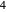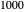Division of whole numbers can be done in two ways. (Long division combines the two.)
keep subtracting the divisor
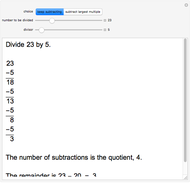
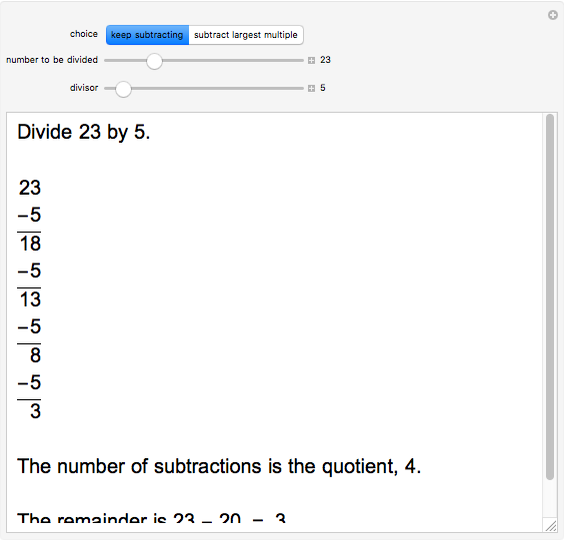
Keep subtracting the divisor until what is left is smaller than the divisor. What is left over is the remainder. The quotient is the number of times you subtracted.
For example, to find 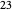 divided by
divided by  , do
, do 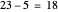 ,
,  ,
, 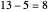 ,
, 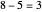 . Stop now because
. Stop now because 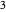 is less than
is less than  . There are four subtractions so the quotient is
. There are four subtractions so the quotient is  . The remainder is
. The remainder is  .
.
Another example: to divide  by
by  , do
, do  ,
, 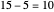 ,
, 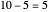 ,
, 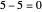 . Stop because
. Stop because  is less than
is less than  . There are four subtractions so the quotient is
. There are four subtractions so the quotient is  . The remainder is
. The remainder is  .
.
Now for division by zero. When you subtract zero from a whole number larger than zero, you get the same whole number back. So you can subtract again and again without making any progress.
For example, to find  divided by
divided by  , do
, do 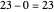 ,
, 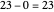 ,
, 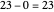 , …, forever. The result is never smaller than
, …, forever. The result is never smaller than 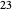 no matter how many times you subtract.
no matter how many times you subtract.
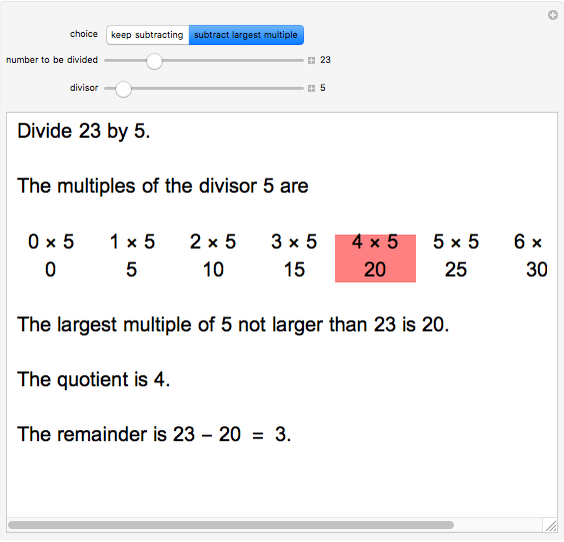
subtract the largest possible multiple of the divisor
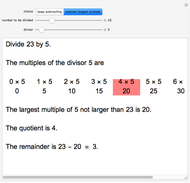
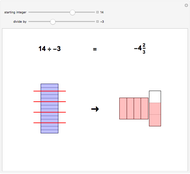
To divide two whole numbers both greater than zero, find the largest multiple of the divisor that is not larger than the number being divided. That multiple is the quotient. The remainder is the difference between the number being divided and the product of the quotient and divisor.
For example, divide 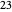 by
by  . The multiples of
. The multiples of  are
are  ,
,  ,
, 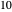 ,
,  ,
, 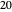 ,
, 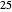 ,
, 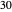 , …. The largest multiple less than
, …. The largest multiple less than  is
is 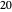 . The quotient is 4 because
. The quotient is 4 because 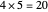 . The remainder is
. The remainder is 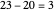 . So
. So 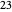 divided by
divided by  is the quotient
is the quotient  with remainder
with remainder 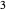 .
.
Another example: to divide  by
by  , do
, do 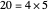 , so the quotient is
, so the quotient is  and the remainder is zero.
and the remainder is zero.
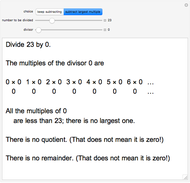
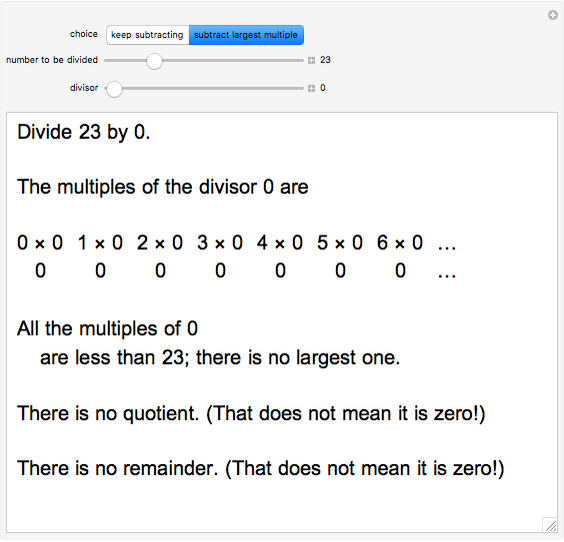
When dividing by zero, all the multiples of zero are zero, so there is no largest one less than the number to be divided.
For example, to divide 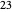 by
by  , all of these multiples are zero and are less than
, all of these multiples are zero and are less than 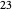 :
: 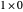 ,
,  ,
, 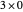 ,
, 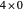 , …,
, …, , …,
, …,  , …. The quotient cannot be the largest of
, …. The quotient cannot be the largest of  ,
, 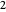 ,
, 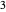 ,
, 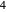 , …,
, …, 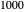 , …,
, …,  , …, because there is no largest.
, …, because there is no largest.
So do not divide by zero!
[less]

 ,
, 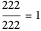 ,
, , and so on, it seems reasonable that
, and so on, it seems reasonable that  should be
should be  , as well.
, as well.  . The number
. The number  is not special;
is not special;  is any number you want.
is any number you want. is not
is not  . Suppose it is
. Suppose it is  instead. Then
instead. Then 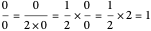 . So
. So  is
is  after all.
after all.  to be, we can use fractions to show it would be anything else. So we cannot give
to be, we can use fractions to show it would be anything else. So we cannot give  any value.
any value.