Domino and Triomino Tilings of a Chessboard

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
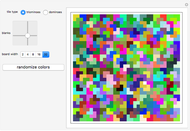
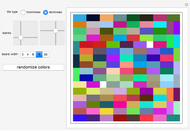
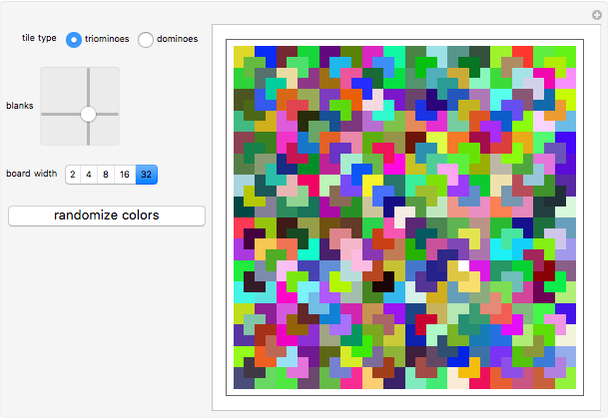
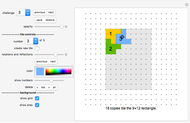
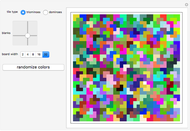
If a single square is removed from a 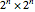 chessboard, then it is always possible to tile the remaining squares using L-shaped triominoes. Likewise, if two opposite-colored squares are removed, then it is always possible to tile the remaining squares using standard dominoes. This Demonstration generates triomino and domino tilings for chessboards of various sizes. Use the controls to select the type of tile used, the size of the board and the location(s) of the blank square(s).
chessboard, then it is always possible to tile the remaining squares using L-shaped triominoes. Likewise, if two opposite-colored squares are removed, then it is always possible to tile the remaining squares using standard dominoes. This Demonstration generates triomino and domino tilings for chessboards of various sizes. Use the controls to select the type of tile used, the size of the board and the location(s) of the blank square(s).
Contributed by: Adam Rumpf (November 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
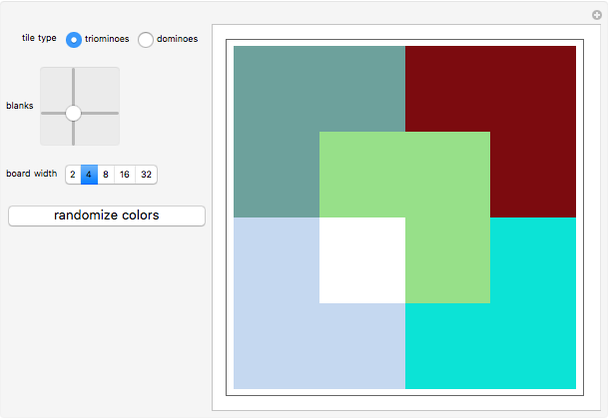
The triomino tiling algorithm is recursive [1]. Given a 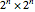 board missing one square, divide it into four
board missing one square, divide it into four 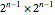 subboards, one of which is missing a square. From the remaining three subboards, remove the square nearest the center of the original board. This results in four
subboards, one of which is missing a square. From the remaining three subboards, remove the square nearest the center of the original board. This results in four 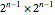 subboards, each missing a square. Three of these missing squares are located near the center of the original board and can easily be tiled by a single L-shaped triomino. To tile the fourth subboard, apply the process recursively until you reach the base case of a
subboards, each missing a square. Three of these missing squares are located near the center of the original board and can easily be tiled by a single L-shaped triomino. To tile the fourth subboard, apply the process recursively until you reach the base case of a 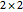 board missing a square, which can obviously be tiled by a single L-shaped triomino.
board missing a square, which can obviously be tiled by a single L-shaped triomino.
For the domino tiling algorithm [2], begin by finding a Hamiltonian cycle on the original board. Removing two squares cuts this cycle into one or two paths. The tiling can be generated by laying down dominoes along the path or paths. It is only possible to complete this domino tiling if the removed squares are of opposite colors [3]. This is because each domino must cover one black square and one white square, so any board that can be tiled must have the same number of squares of each color.
References
[1] F. E. Su et al. "Inductive Tiling," Math Fun Facts. (Oct 31, 2017) www.math.hmc.edu/funfacts.
[2] J. Kun, "Tiling a Chessboard with Dominoes (Opposite Colors Removed)," Math ⋂ Programming (blog). (Oct 31, 2017) jeremykun.com/2011/11/18/tiling-a-chessboard-2.
[3] F. E. Su et al. "Dominoes on a Chessboard," Math Fun Facts. (Oct 31, 2017) www.math.hmc.edu/funfacts.
Permanent Citation