Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Domino Substitution Tilings

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

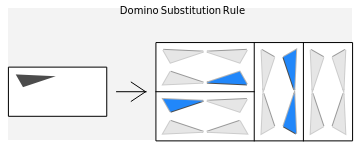
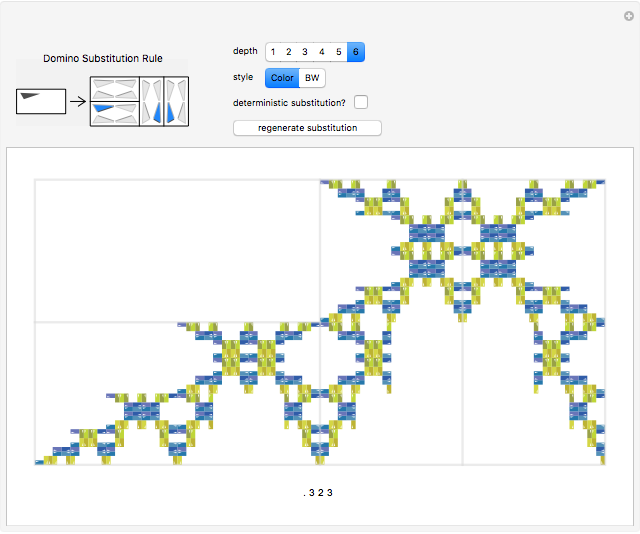
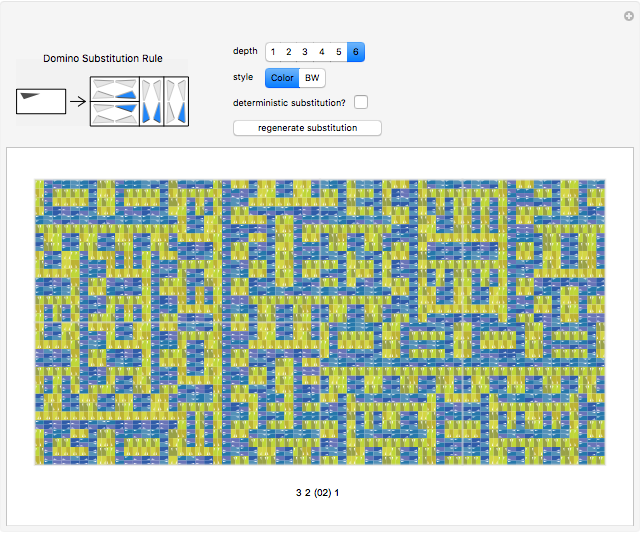
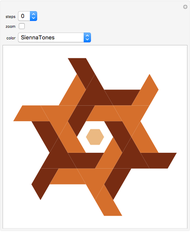
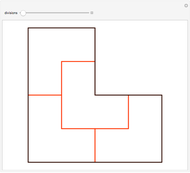
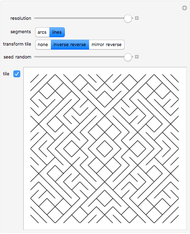
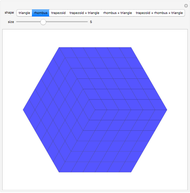
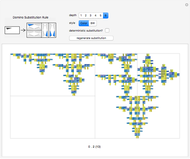
Tiling substitution rules specify how to fill and then subdivide a tile into copies of itself. Iterating these rules, we can form larger and larger "supertiles" and ultimately define substitution tilings, which are divisions of the plane into infinite hierarchies of supertiles. The configuration shown here, of four dominoes (2×1 rectangles, also known as dimers) forming a larger one, does not give a well-defined substitution rule: in order to iterate such a rule, we must further specify how the smaller dominoes are oriented in the large one, possibly with several choices.

Contributed by: Chaim Goodman-Strauss (June 2016)
Open content licensed under CC BY-NC-SA

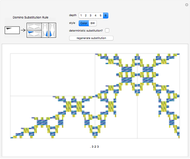
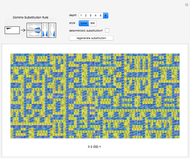
Snapshots

Details

The forthcoming paper "Lots of Aperiodic Sets of Tiles" gives, for each substitution rule in this Demonstration, a set of marked tiles that can form only tilings with the structure generated by the rule, increasing the number of explicitly described aperiodic sets of tiles several hundredfold. This Demonstration illustrates the rich variety of these systems.

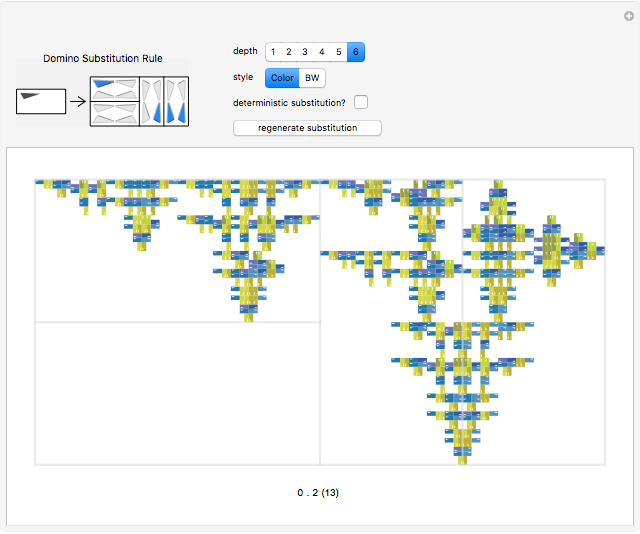
The substitution rule is specified by the 16 triangular buttons at the top left. The depth of the substitution is controlled by a selector. The tiling may be displayed in black and white or in color.

Deterministic substitution rules allow, at most, one choice of orientation per domino. Otherwise, choices are made randomly, and it is interesting to regenerate the supertile.

The code at the bottom of the Manipulate is used to refer to specific rules.

References

[1] Wikipedia. "Substitution Tiling." (Jun 27, 2016) en.wikipedia.org/wiki/Substitution_tiling.

[2] Tilings Encyclopedia. "Substitution." (Jun 27, 2016) tilings.math.uni-bielefeld.de/glossary/substitution.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send