Doped Silicon Semiconductors

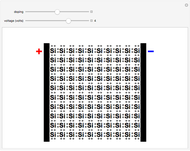
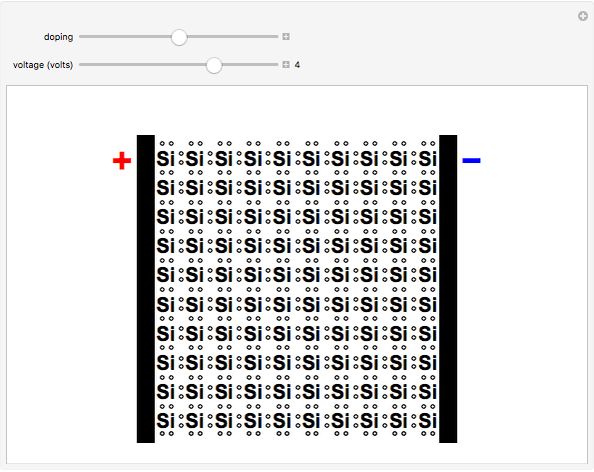
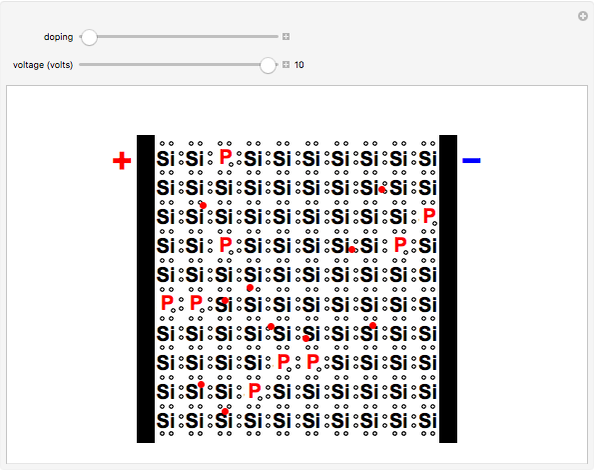
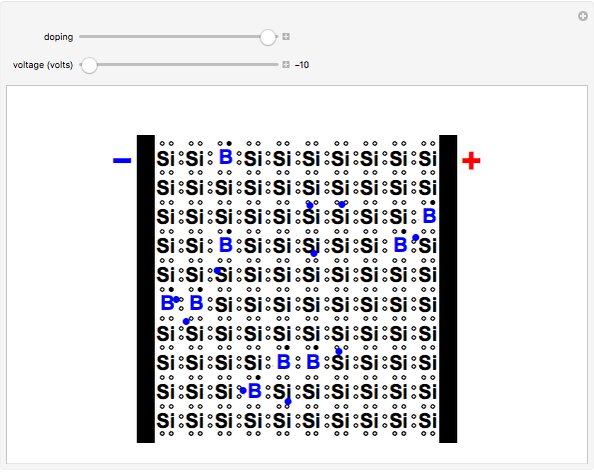
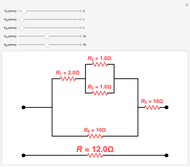
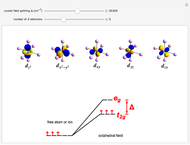
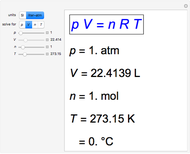
In a pure silicon crystal, each Si atom has four valence electrons that can form Lewis octets with four other atoms. A schematic two-dimensional representation of the crystal is shown. When an occasional electron is shaken loose by thermal excitation or a crystalline defect, silicon becomes a weak conductor of electricity (not shown). Much more important to the semiconductor industry are extrinsic semiconductors, in which the Si crystal is doped with impurity atoms, usually at concentrations of several parts per million. For example, Si can be doped with P (or As or Sb) atoms, which have five valence electrons. The fifth electron is not needed for bonding and becomes available as a current carrier. This is known as an n-type semiconductor. The mobile electrons are shown in red. If the Si is instead doped with B (or Ga or Al), which have only three valence electrons, this leaves an electron vacancy or positive hole, shown as a black circle. Positive holes can likewise act as current carriers, to produce p-type semiconductors. The mobile holes are shown in blue. The "doping" slider enables you to continuously (in concept) transform the crystal from a p-type to an n-type semiconductor.