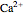Double Refraction by a Uniaxial Crystal

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
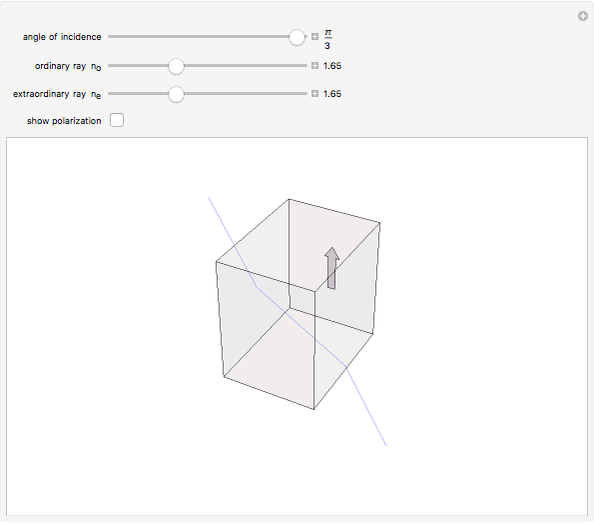
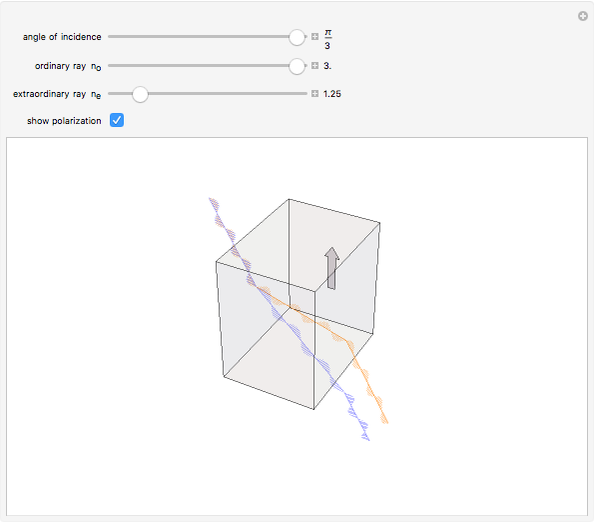
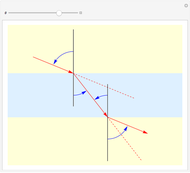
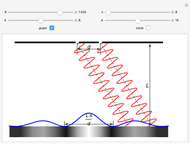
Crystalline materials can have different indices of refraction in different crystallographic directions. Crystals belonging to the hexagonal, tetragonal, or rhombohedral classes are uniaxial, in that they possess a unique optical axis, most often coincident with the crystallographic  axis. Light traveling through such an anisotropic medium can exhibit double refraction or birefringence, in which an unpolarized incident light ray splits into two polarized rays with mutually perpendicular planes of vibration. The ray with its electric field vibrating perpendicular to the optical axis is called the ordinary ray, and is characterized by an index of refraction
axis. Light traveling through such an anisotropic medium can exhibit double refraction or birefringence, in which an unpolarized incident light ray splits into two polarized rays with mutually perpendicular planes of vibration. The ray with its electric field vibrating perpendicular to the optical axis is called the ordinary ray, and is characterized by an index of refraction 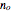 . The ray that vibrates parallel to the optical axis is called the extraordinary ray, with its index of refraction designated
. The ray that vibrates parallel to the optical axis is called the extraordinary ray, with its index of refraction designated  . The birefringence is the difference Δ
. The birefringence is the difference Δ , which can be positive or negative.
, which can be positive or negative.
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: conventional refraction when  and
and  are equal
are equal
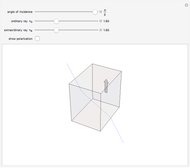
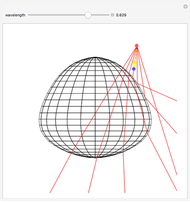
Snapshot 2: double refraction by a hypothetical crystal with large birefringence
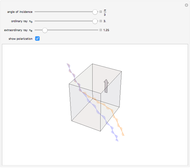
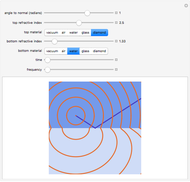
Snapshot 3: same crystal with polarizations shown
Permanent Citation