Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

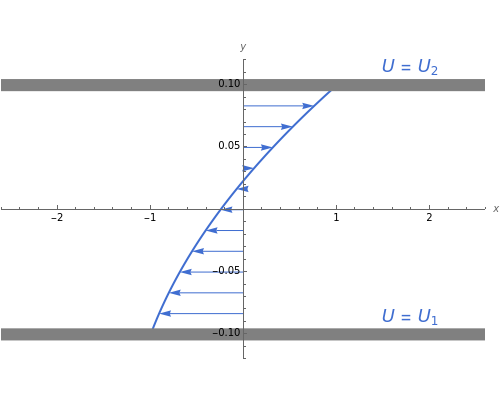
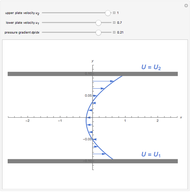
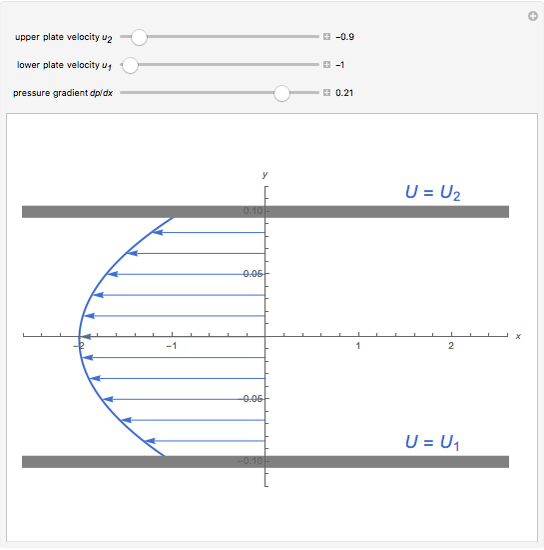
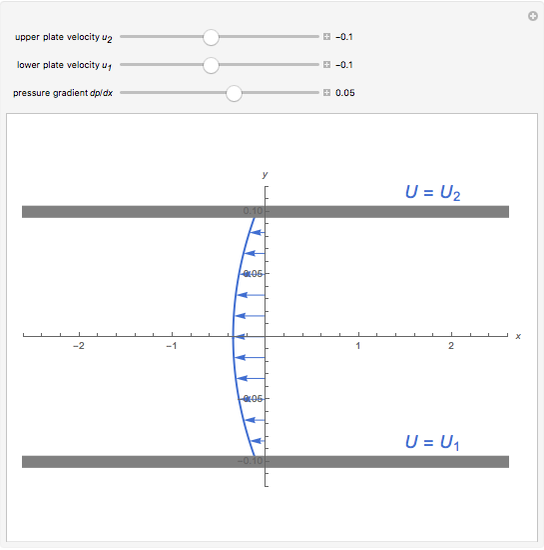
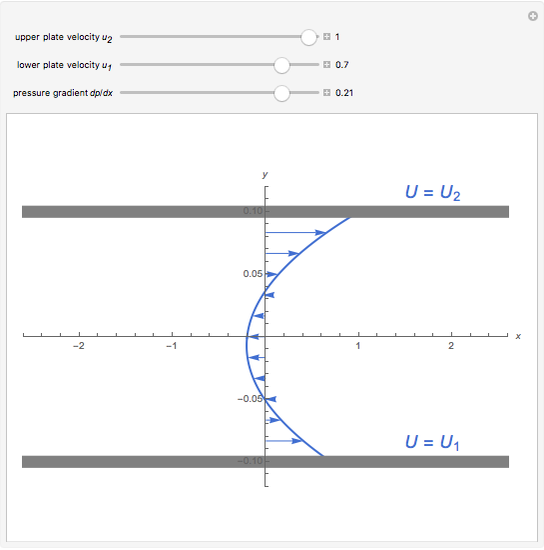
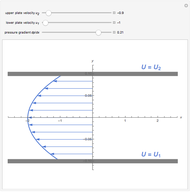
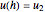Double-Sided Couette Flow

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

The permanent laminar flow of an incompressible viscous fluid in the space between two parallel plates can be described by a linear ODE for 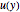: 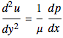, where is the dynamic viscosity of the fluid and 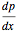is the pressure gradient.

[more]

The boundary conditions are:

(lower plate velocity),

(upper plate velocity).

This problem has an analytic solution:

that varies as a function of the pressure gradient and the upper and lower plate velocity.

[less]

Contributed by: David Gerhardinger (March 2011)
Based on a program by: William C. Guttner
Open content licensed under CC BY-NC-SA

Snapshots

Details

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send