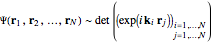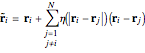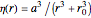Dressed Multi-Particle Electron Wave Functions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
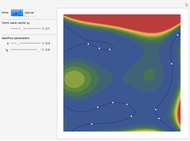
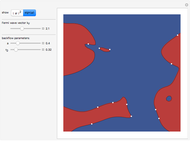
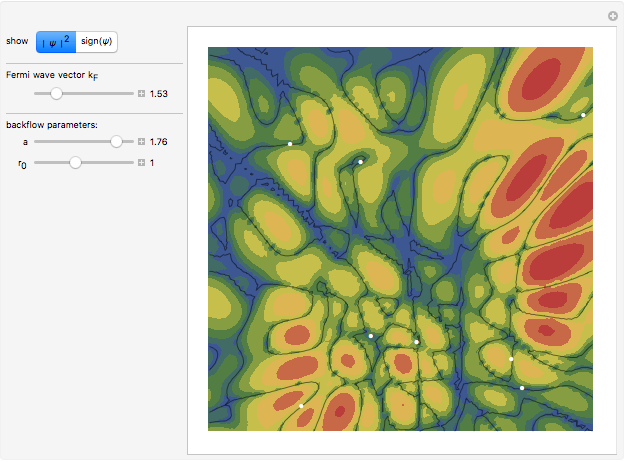
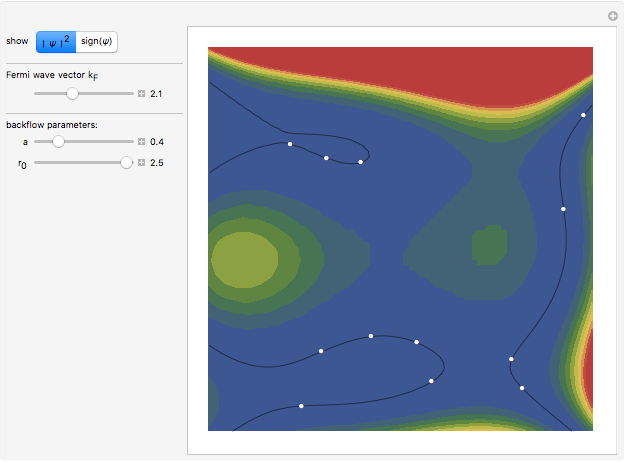
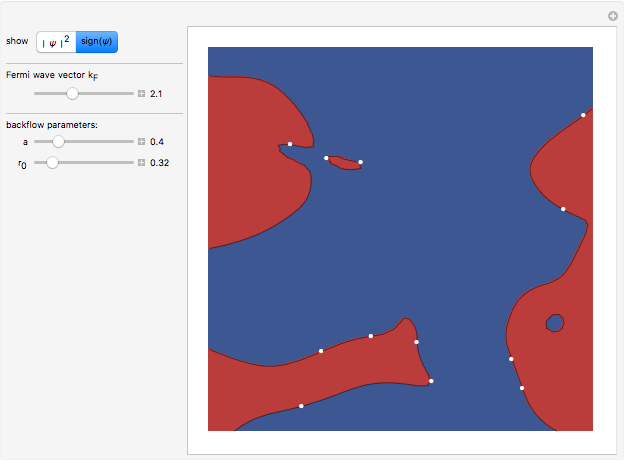
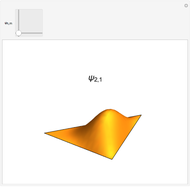
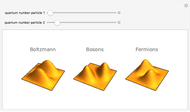
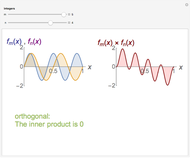
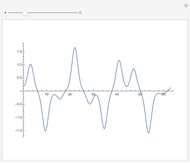
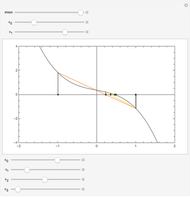
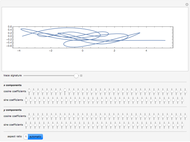
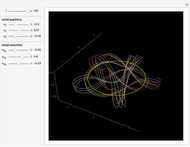
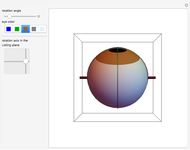
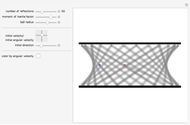
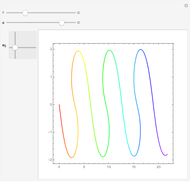
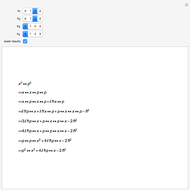
The detailed structure of many‐particle wave functions of electrons (such as in any conductor, semiconductor, or superconductor) is a fascinating current physics problem that still contains many unexplored aspects. For noninteracting fermions, the stationary wave function can be represented as a Slater determinant
[more]
Contributed by: Michael Trott with permission of Springer (March 2011)
From: The Mathematica GuideBook for Programming, second edition by Michael Trott (© Springer, 2008).
Open content licensed under CC BY-NC-SA
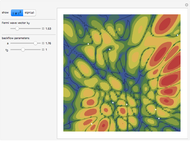
Snapshots
Details
For the details of the underlying physics, see: F. Krüger and J. Zaanen, "Fermionic Quantum Criticality and the Fractal Nodal Surface" and references therein.
Permanent Citation