Drilling a Hexagonal Hole

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
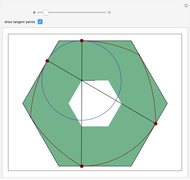
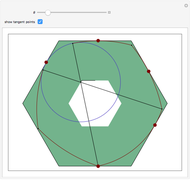
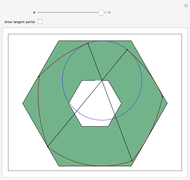
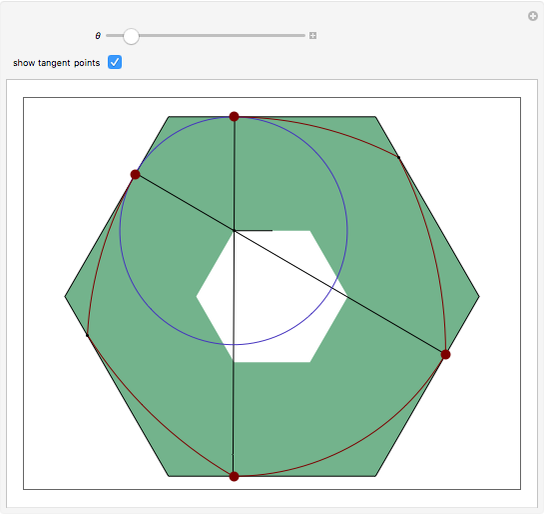
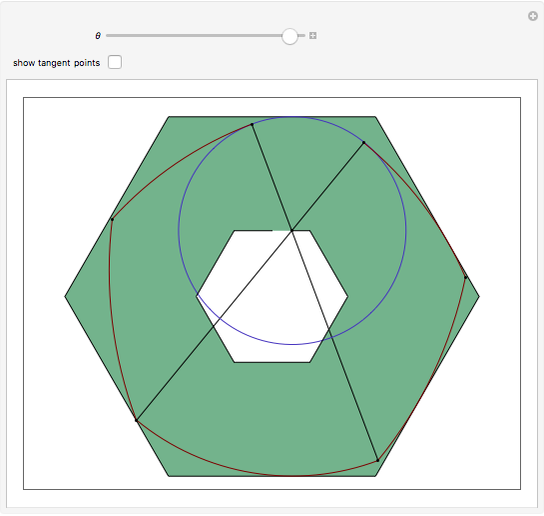
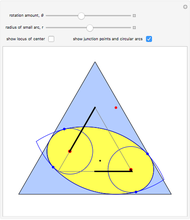
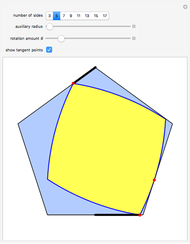
By using a suitable roller restricted to rotate inside a hexagon, one can force a point on the roller to trace out an exact hexagonal path. This construction is due to the authors, inspired by a 1939 construction for a perfect square-hole drill. In this case, though, the roller does not touch all six sides of the hexagon, but it always touches sufficiently many sides to ensure rigidity within the ambient hexagon. As the roller rotates within the ambient hexagon, the center of the blue circle has a locus that is an exact hexagon. The red points are the points on the roller that touch the hexagon and enforce rigidity within it.
Contributed by: Barry Cox (University of Wollongong, Australia) and Stan Wagon (Macalester College, USA) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
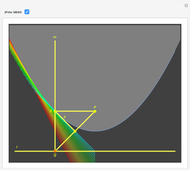
The construction of the roller proceeds as follows.
1. Draw a unit hexagon centered at 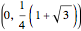 .
.
2. Get the top arc using a circle of radius 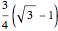 centered at (0,1).
centered at (0,1).
3. Get the bottom arc using a circle of radius 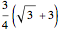 centered at (0,1). Let
centered at (0,1). Let 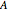 be the point of intersection of the bottom arc and the hexagon.
be the point of intersection of the bottom arc and the hexagon.
4. Get the northwest arc using center 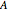 and radius
and radius 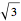 . The northeast arc is similar.
. The northeast arc is similar.
5. Get the southwest arc using center  and radius
and radius 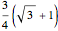 . The northeast arc is similar.
. The northeast arc is similar.
6. Use the intersection of the northwest and southwest arcs to define the upper termination of those arcs; the east side is similar.
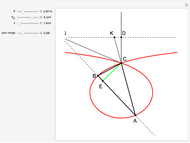
As  increases from 0 to
increases from 0 to 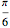 the entire roller is rotated clockwise through
the entire roller is rotated clockwise through  and then translated leftward so as to place
and then translated leftward so as to place 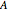 on the hexagon. For the first 0.049 radians of this rotation there are only four points of contact: the upper and lower points guarantee that there is no up-down motion, and the two points on the southwest and southeast sides guarantee rigidity in the left-right direction. After this critical value of
on the hexagon. For the first 0.049 radians of this rotation there are only four points of contact: the upper and lower points guarantee that there is no up-down motion, and the two points on the southwest and southeast sides guarantee rigidity in the left-right direction. After this critical value of  there are five points of contact. As the rotation continues, symmetry governs the patterns and there are always four or five points of contact, sufficient to ensure rigidity.
there are five points of contact. As the rotation continues, symmetry governs the patterns and there are always four or five points of contact, sufficient to ensure rigidity.
Permanent Citation