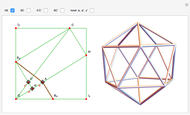
Dual Billiards

Initializing live version

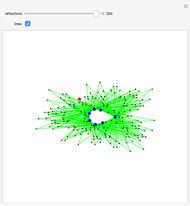
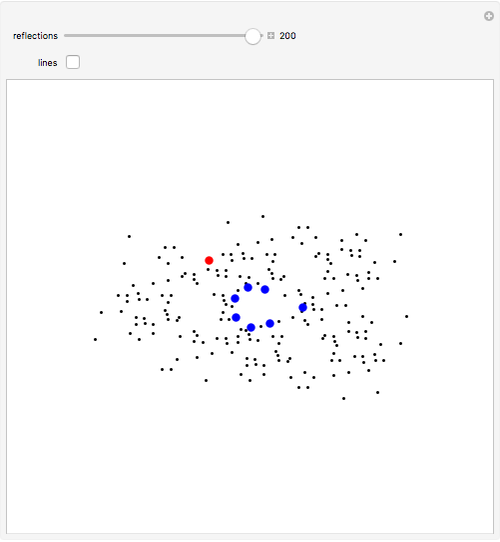
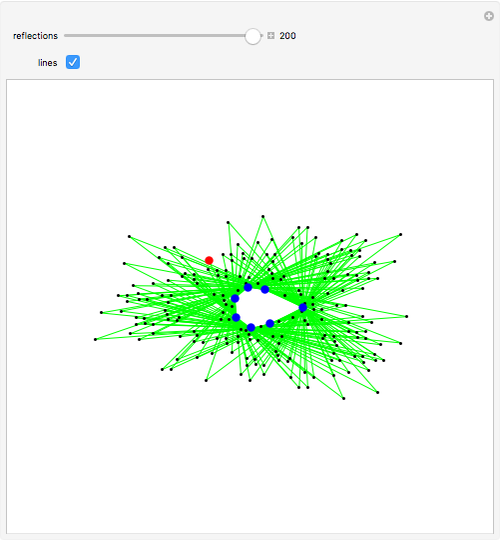
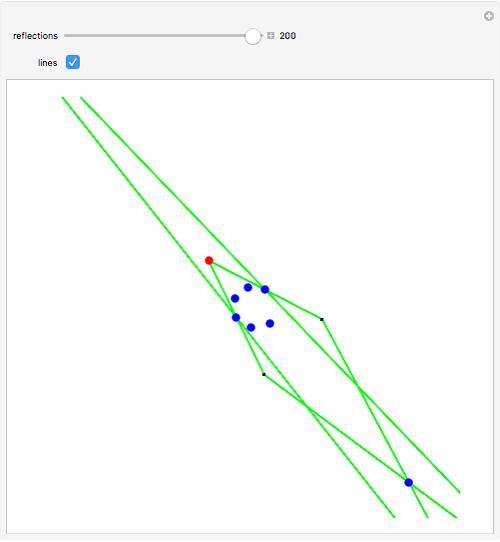
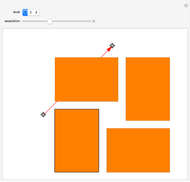
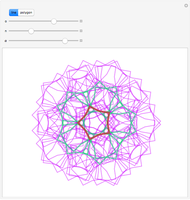
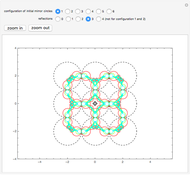
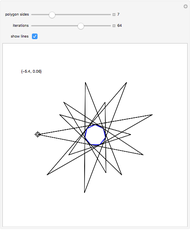
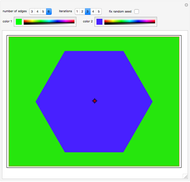
The red point looks at the blue points and is reflected in the one furthest to its right; the process repeats with the new reflected point.

Contributed by: George Beck (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

S. Tabachnikov, Geometry and Billiards (Mathematics Advanced Study Semesters), Providence, RI: American Mathematical Society, 2005.


Feedback (field required)

Email (field required)	Name

Occupation	Organization

Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback. Send