Duopoly Model in 3D

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Duopoly (oligopoly with two firms) is a topic that is equally important for the game-theoretic approach to economic analysis and for traditional microeconomic exposition of market structures with demand and supply curves. Ironically, these two views are rarely presented together in textbooks. The purpose of this Demonstration is to show the straightforward connection between the supply-demand model and the game-theoretic representation of reaction functions in a classical duopoly setting.
Contributed by: Timur Gareev (October 2015)
Immanuel Kant Baltic Federal University
Open content licensed under CC BY-NC-SA
Snapshots
Details
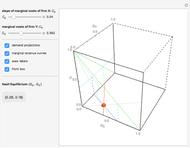
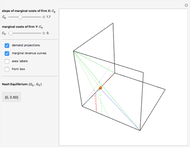
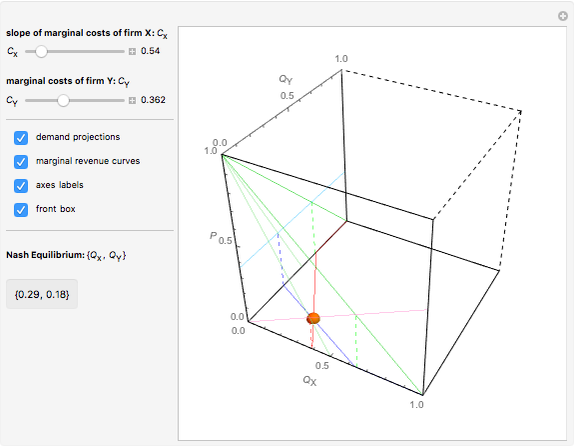
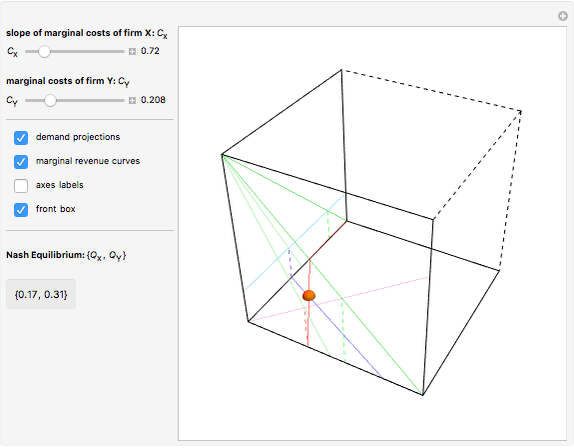
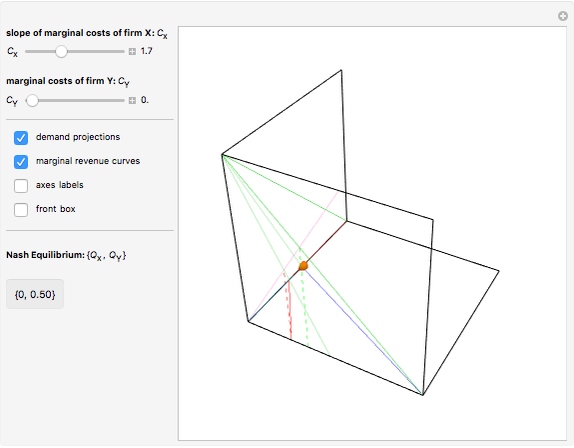
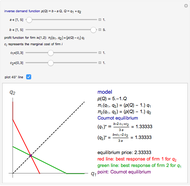
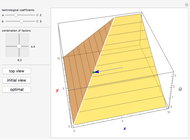
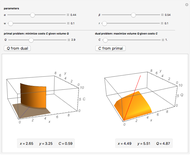
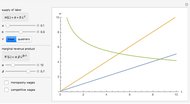
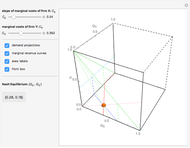
We build a 3D model of market demand (in a simple form, 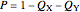 ) on a duopoly market. Two firms
) on a duopoly market. Two firms 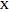 and
and 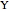 produce the same good with total quantity defined as
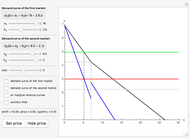
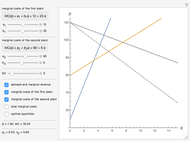
produce the same good with total quantity defined as 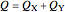 , but may have different cost functions (you can control the cost of production for the firms with the sliders). Both firms also simultaneously decide on what quantity of the good to produce. They make choices according to their respective reaction functions. Equilibrium production given the demand and costs structure is defined by the intersection of reaction functions. For this simple model, such an intersection point corresponds to a unique Nash equilibrium, here represented by an orange sphere. So this is a canonical case (and, perhaps, one of the simplest) of strategic interactions as far as each firm's decision depends on the choice of the other firm. You can see that changing the marginal costs of one firm leads to a shift of its reaction function curve that in its turn changes the equilibrium quantities for both firms. It is also interesting to see that above some cost level we have a "corner" solution where a "high-cost" firm produces nothing in equilibrium. In this linear case, the other firm produces as if it were a monopolist on the market. If both firms produce with zero costs, we have a classical solution
, but may have different cost functions (you can control the cost of production for the firms with the sliders). Both firms also simultaneously decide on what quantity of the good to produce. They make choices according to their respective reaction functions. Equilibrium production given the demand and costs structure is defined by the intersection of reaction functions. For this simple model, such an intersection point corresponds to a unique Nash equilibrium, here represented by an orange sphere. So this is a canonical case (and, perhaps, one of the simplest) of strategic interactions as far as each firm's decision depends on the choice of the other firm. You can see that changing the marginal costs of one firm leads to a shift of its reaction function curve that in its turn changes the equilibrium quantities for both firms. It is also interesting to see that above some cost level we have a "corner" solution where a "high-cost" firm produces nothing in equilibrium. In this linear case, the other firm produces as if it were a monopolist on the market. If both firms produce with zero costs, we have a classical solution 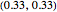 that gives the total production
that gives the total production 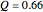 that is more than in the monopoly case
that is more than in the monopoly case 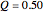 but less than the possible
but less than the possible 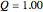 .
.
Permanent Citation
"Duopoly Model in 3D"
http://demonstrations.wolfram.com/DuopolyModelIn3D/
Wolfram Demonstrations Project
Published: October 13 2015