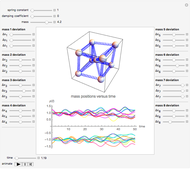
Dynamics of a Cube-Shaped Mass-Spring Network

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
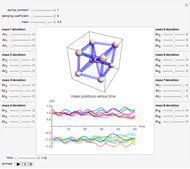
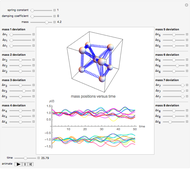
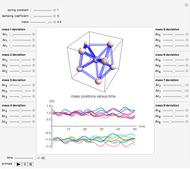
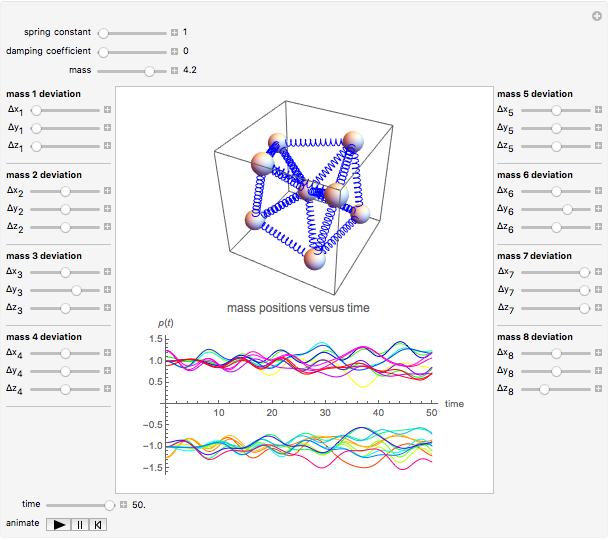
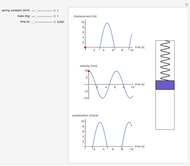
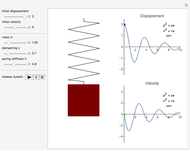
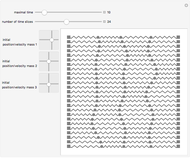
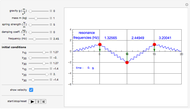
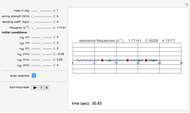
This Demonstration shows the dynamics of a 3D spring-mass system consisting of nine identical masses arranged in a body-centered cube and connected by 20 springs. The effect of gravity is assumed to be negligible (as in outer space, for example). The springs are assumed to have the same force constant and damping coefficient. The mass at the center is fixed at the origin, while the eight outer masses can be moved.
[more]
Contributed by: Te-yuan Chyou (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The dynamics of the system can be modeled using Lagrangian mechanics.
Let 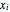 be the position of mass
be the position of mass  in 3D. The total kinetic energy due to the motion of the masses is:
in 3D. The total kinetic energy due to the motion of the masses is:
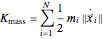 .
.
Define  as the graph of 20 mass-to-mass spring linkages. The total potential energy due to deformation of all springs is:
as the graph of 20 mass-to-mass spring linkages. The total potential energy due to deformation of all springs is:
 .
.
Hence the Lagrangian expression is:
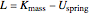 .
.
The total negative work due to spring damping can be written as a Rayleigh dissipative function:
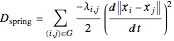 .
.
Hence the equations of motion for the masses are given by the Euler–Lagrange equations:
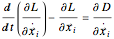 .
.
Permanent Citation