Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Dynamics of an Elementary Cellular Automaton

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

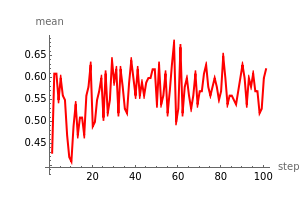
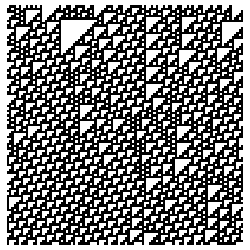
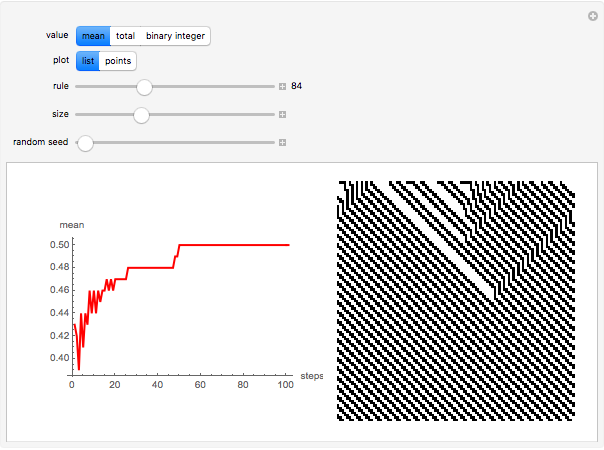
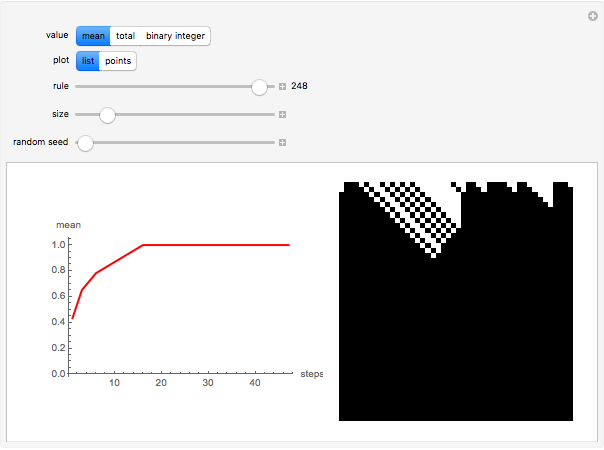
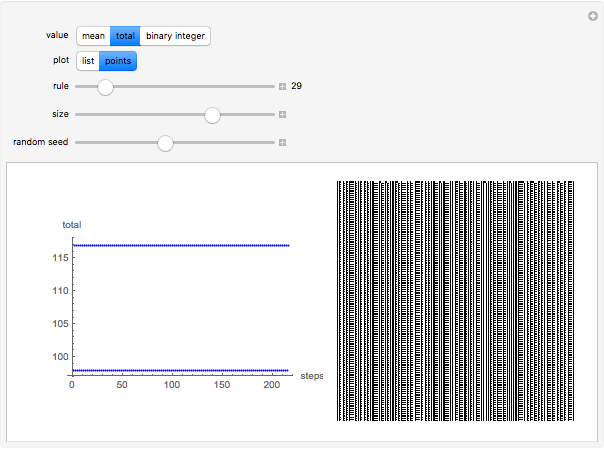
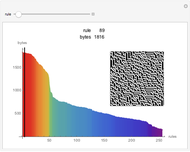
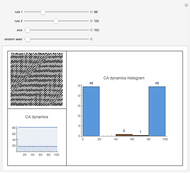
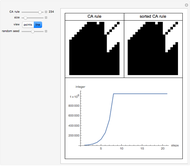
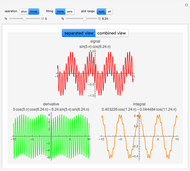
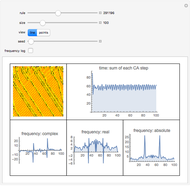
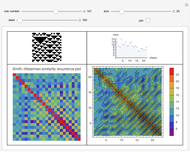
The dynamic of a cellular automaton (CA) evolution with a random initial condition can be studied by calculating the value of the mean, the total (sum), or the base conversion from binary to decimal for each step.

[more]

The evolution of CA rules class 1 tends to stabilize to just one value.

The evolution of CA rules class 2 tends to stabilize or to be periodic.

The evolution of CA rules class 3 tends to be chaotic (noisy).

The evolution of CA rules class 4 tends to be a mix of chaotic and periodic, with local repetitive distributions.

Transitory states can occur in the CA evolution depending on the initial condition.

[less]

Contributed by: Daniel de Souza Carvalho (March 2011)
Open content licensed under CC BY-NC-SA

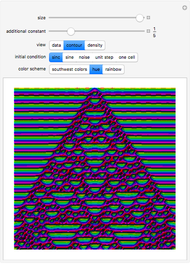
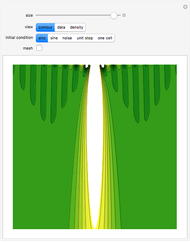
Snapshots

Details

detailSectionParagraph
Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send