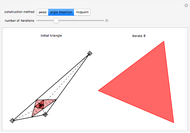
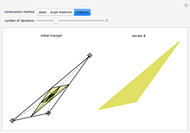
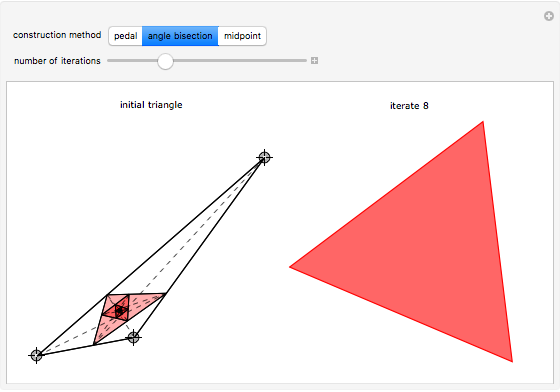
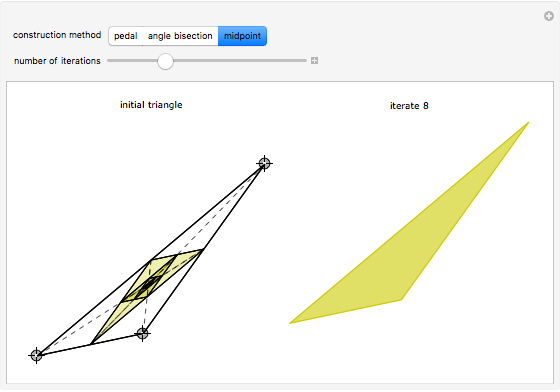
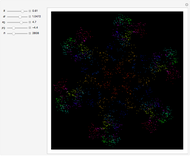
Given any triangle, we may construct a new triangle by choosing vertices from the edges of the original. The process may be iterated to generate a sequence of triangles. The dynamics of this sequence depends strongly on how the new vertices are chosen. If the three new vertices are the midpoints of the original triangle, then the new triangle will be similar to the original; we may regard any triangle as a fixed point of the dynamical system. If we choose the new vertices by bisecting the angles of the original triangle and find the intersections of these angles with the opposite sides, then the sequence of triangles will converge rapidly to an equilateral triangle. Finally, if we drop a perpendicular from each vertex to the opposite side, we find the vertices of a triangle called the pedal triangle of the original. The sequence of pedal iterates need not lie inside the original triangle and is generally chaotic.