Edwards's Solution of Pendulum Oscillation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
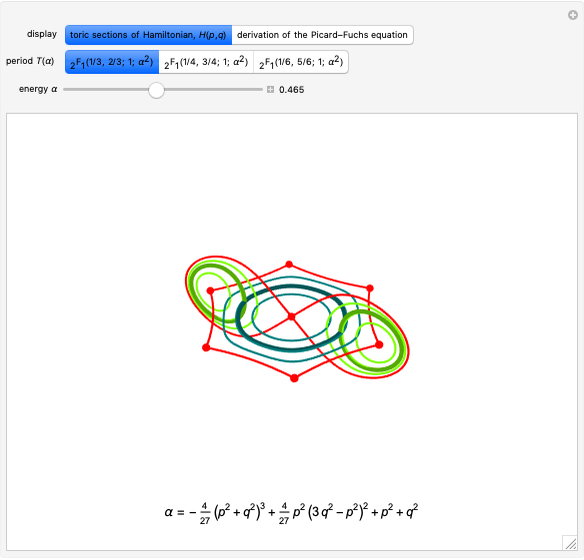
The masterful derivation by Harold Edwards [1] finally brings the vision of Abel to the wider audience it deserves. The article describes a constructive approach for improving computations along elliptic curves. The new and simple addition rules of [1, Part II] have been widely appreciated, while the calculus of [1, Part III] remains underutilized. As with the much earlier Weierstrass  function, the Edwards
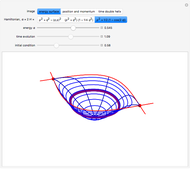
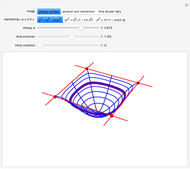
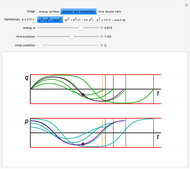
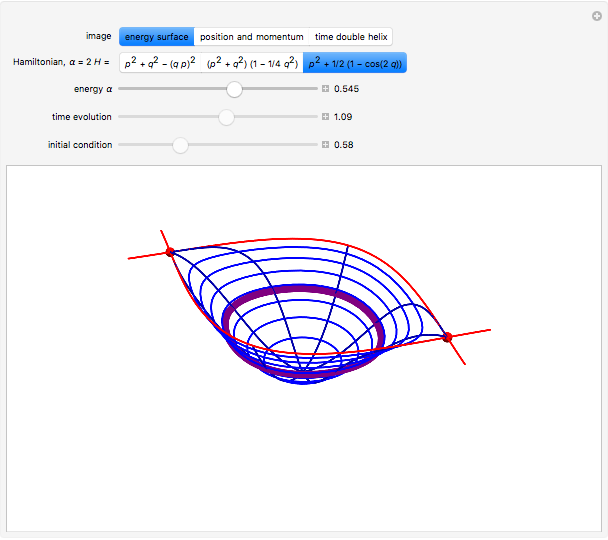
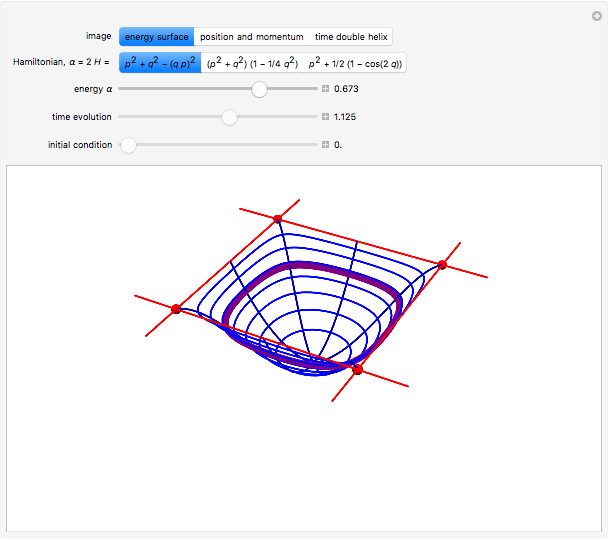
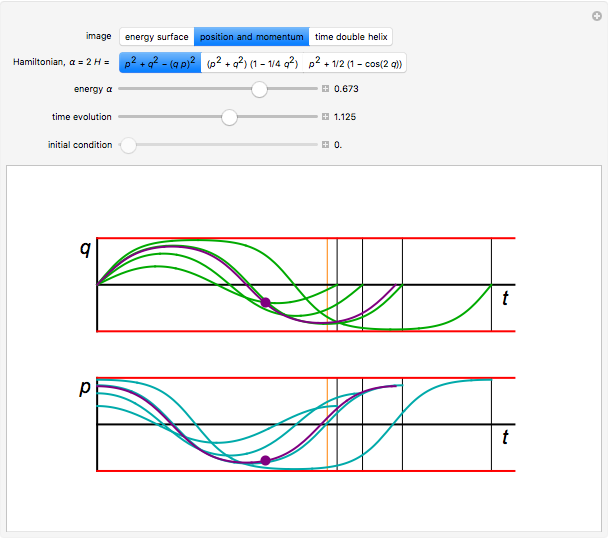
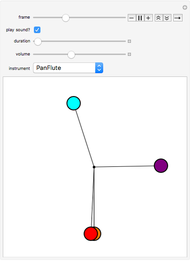
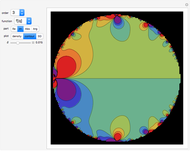
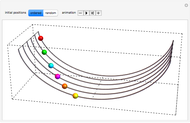
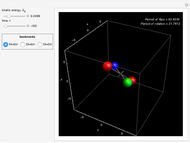
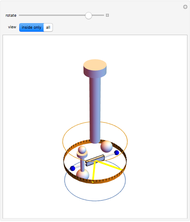
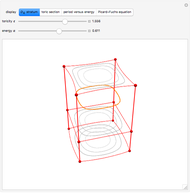
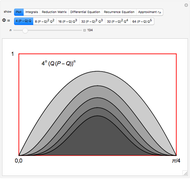
function, the Edwards  function determines time-dependent solutions for a range of interesting Hamiltonian systems [2]. This Demonstration shows three interrelated examples, including one that describes the oscillation of a plane pendulum. Edwards
function determines time-dependent solutions for a range of interesting Hamiltonian systems [2]. This Demonstration shows three interrelated examples, including one that describes the oscillation of a plane pendulum. Edwards  function is truly an amazing and beautiful, doubly-periodic, meromorphic function!
function is truly an amazing and beautiful, doubly-periodic, meromorphic function!
Contributed by: Brad Klee (March 2018)
Open content licensed under CC BY-NC-SA
Details
For precision and accuracy tests, see commented code above. For an in-depth derivation of the solution, see [2].
References
[1] H. M. Edwards, "A Normal Form for Elliptic Curves," Bulletin of the American Mathematical Society, 44, 2007 pp. 393–422. doi:10.1090/S0273-0979-07-01153-6.
[2] B. Klee, "An Alternative Theory of Simple Pendulum Libration", https://github.com/bradklee.
Snapshots
Permanent Citation