Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Effect of a 3x3 Singular Transformation Matrix on 3D Space

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

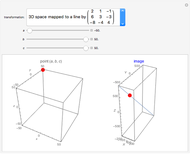
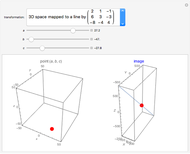
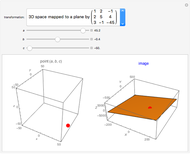
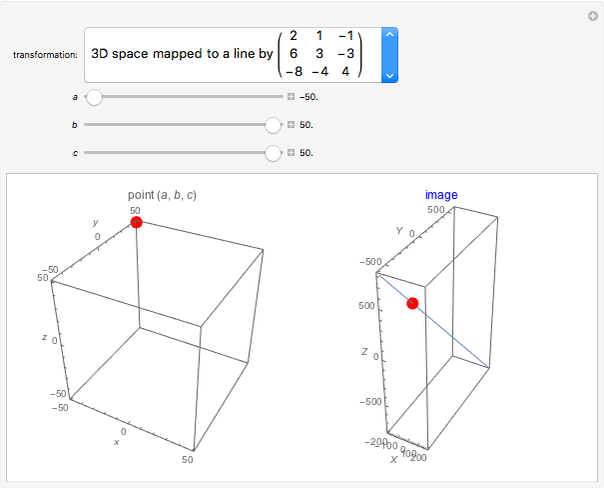
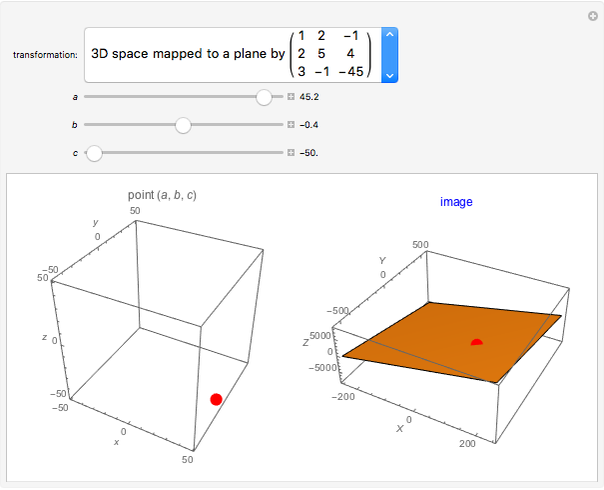
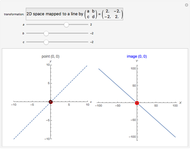
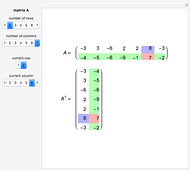
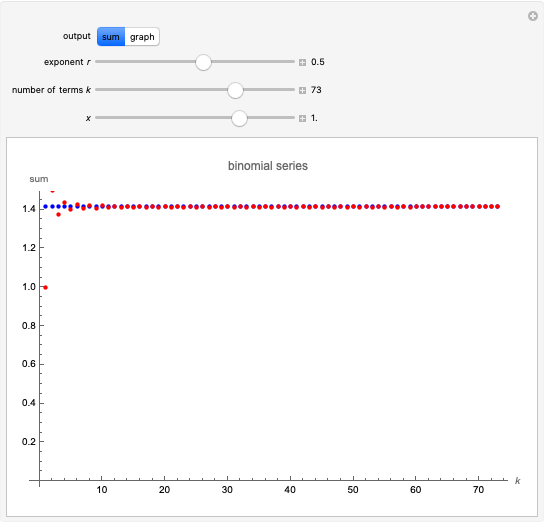
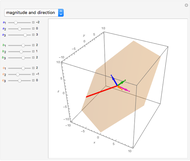
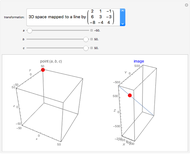
This Demonstration shows the effect of two 3×3 nonzero singular transformation matrices on 3D space: all points in 3D space are either mapped to a line or plane passing through the origin. Use the sliders to vary the coordinates of the point in the plot on the left and observe its corresponding image point in the plot on the right.

[more]

When the three columns of the singular matrix are all scalar multiples of one another, the image of is a line; otherwise it is a plane.

[less]

Contributed by: Roberta Grech (May 2013)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Transformation matrices are usually studied by pure math students in high school in certain countries.

Reference

[1] L. Bostock, S. Chandler, and C. Rourke, Further Pure Mathematics, Cheltenham, UK: Stanley Thornes, 1990.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send