Effective Resistance between an Arbitrary Pair of Nodes in a Graph

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
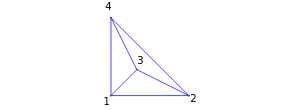
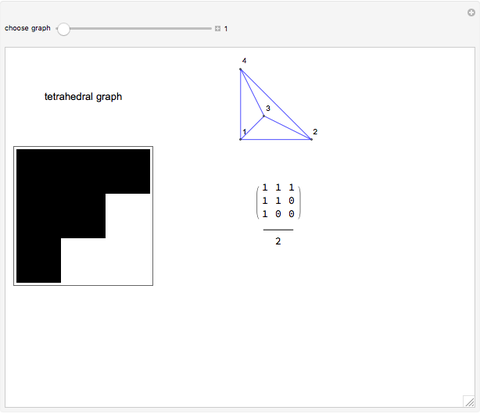
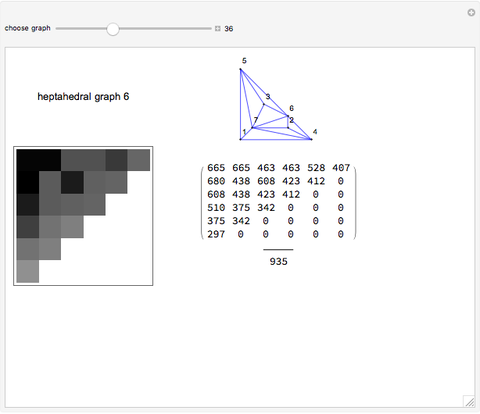
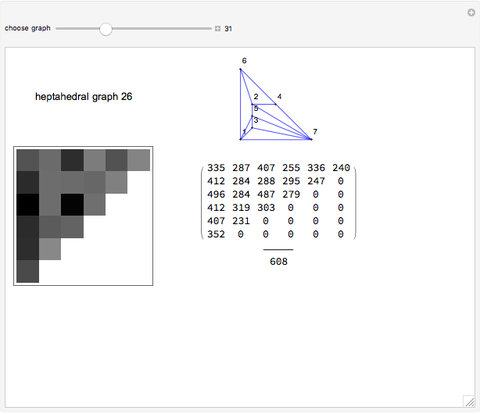
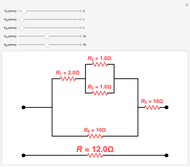
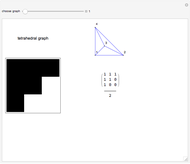
The Demonstration finds the effective resistance between arbitrary pairs of nodes in an electrical resistor circuit. Each edge in the circuit can be thought of as having one unit of resistance. The grid shows how the effective resistance between any two pairs of nodes (labeled) in the circuit fluctuates, depending on the number of resistances (or links) between the pair of nodes.
Contributed by: Arnab Kar (June 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
From the adjacency matrix 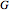 (gmat in the code) of a graph with
(gmat in the code) of a graph with 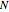 nodes, the matrix
nodes, the matrix 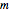 is constructed:
is constructed:
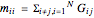 ,
,
 .
.
Denote the nodes between which the effective resistance is computed as  and
and 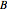 . The matrix
. The matrix 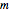 is rearranged into a block structure:
is rearranged into a block structure: 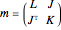 , where
, where 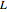 is a
is a 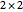 matrix carrying the resistance information for the nodes
matrix carrying the resistance information for the nodes  and
and 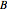 ,
, 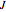 is a
is a 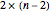 matrix, and
matrix, and 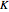 is a
is a  matrix. By completion of squares, the effective resistance between nodes
matrix. By completion of squares, the effective resistance between nodes  and
and 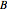 is computed after integrating out the information of the other vertices to get the matrix
is computed after integrating out the information of the other vertices to get the matrix 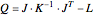 . The inverse of an off-diagonal element in this matrix
. The inverse of an off-diagonal element in this matrix  gives the effective resistance between a pair of nodes. You can think of the off-diagonal element as the cross term between nodes
gives the effective resistance between a pair of nodes. You can think of the off-diagonal element as the cross term between nodes  and
and 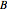 , which is the inverse of the effective resistance after the other vertices are integrated out.
, which is the inverse of the effective resistance after the other vertices are integrated out.
References
[1] Wikipedia. "Resistance Distance." (May 24, 2016) en.wikipedia.org/wiki/Resistance_distance.
[2] Wikipedia. "Completing the Squares." (May 24, 2016) en.wikipedia.org/wiki/Completing_the_square.
[3] F. Y. Wu, "Theory of Resistor Networks: The Two-Point Resistance," Journal of Physics A: Mathematical and General, 37(26), 2004, pp. 6653–6673. doi:10.1088/0305-4470/37/26/004.
Permanent Citation