Ehrenfest's Double-Urn Game

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
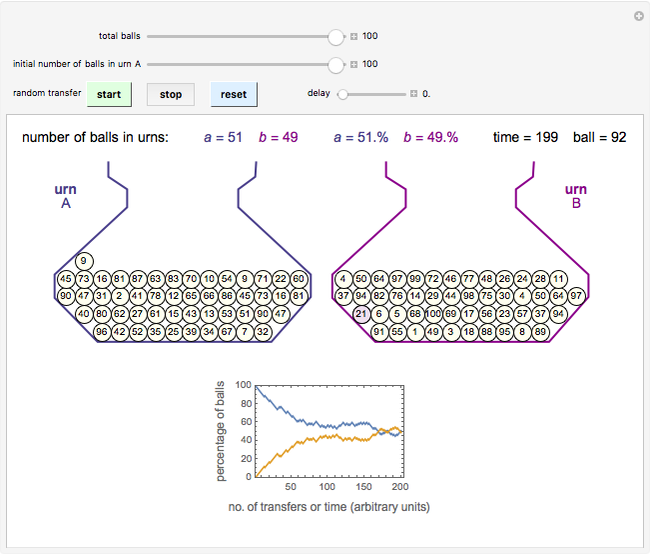
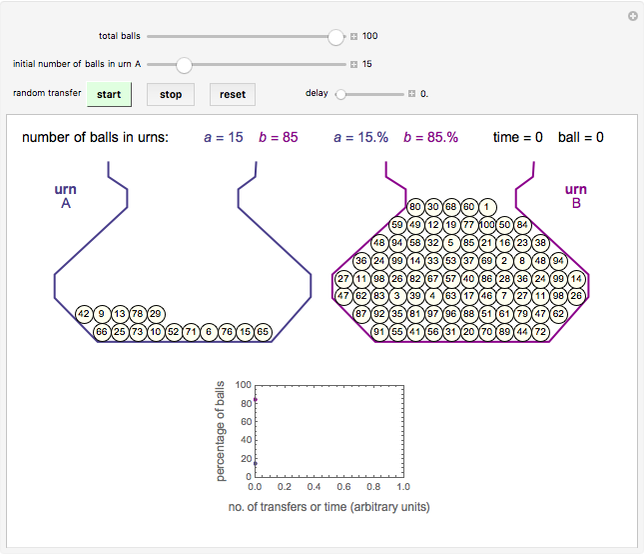
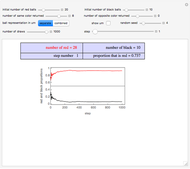
Statistical irreversibility as an explanation of the direction of time's arrow has been presented in various ways. The principle of statistical irreversibility postulates that some states that are physically possible will not occur because of extremely low probability [1, 2]. The physicist Paul Ehrenfest (1880–1933) showed this elegantly in a game with one simple rule: there are  balls unequally or equally divided between two urns A and B. A ball is chosen at random. If it happens to be in urn A, it moves to urn B, and if it happens to be in urn B, it moves to urn A. The process is repeated, and it is seen that after a while, regardless of the total number of balls and the balls' initial distribution between the urns, the system reaches a dynamic equilibrium around
balls unequally or equally divided between two urns A and B. A ball is chosen at random. If it happens to be in urn A, it moves to urn B, and if it happens to be in urn B, it moves to urn A. The process is repeated, and it is seen that after a while, regardless of the total number of balls and the balls' initial distribution between the urns, the system reaches a dynamic equilibrium around 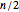 . Also, unless the total initial number of balls in the two urns is very small, or the numbers in each urn are about equal, the original distribution is unlikely to be restored, regardless of how long one waits.
. Also, unless the total initial number of balls in the two urns is very small, or the numbers in each urn are about equal, the original distribution is unlikely to be restored, regardless of how long one waits.
Contributed by: Mark D. Normand and Micha Peleg (September 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
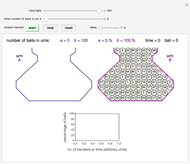
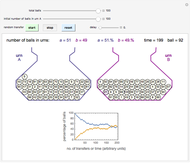
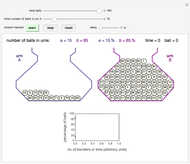
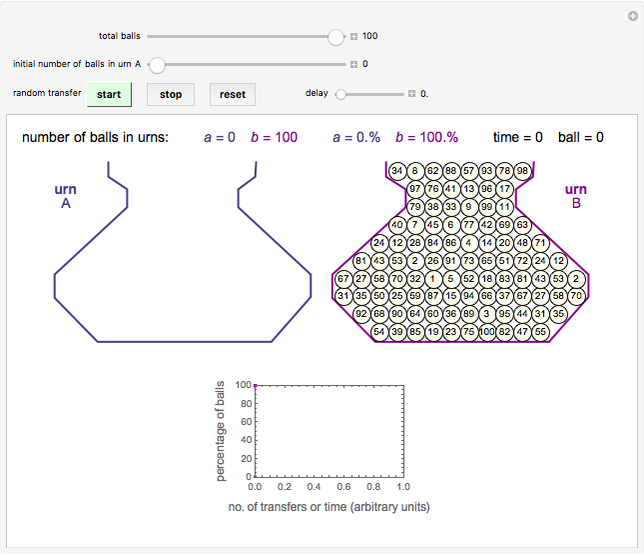
Ehrenfest's double-urn game starting with:
Snapshot 1: one empty urn
Snapshot 2: one empty urn after about 200 transfers
Snapshot 3: a lot of balls, most in urn B
Snapshot 4: a lot of balls, most in urn B, after about 100 transfers
Snapshot 5: a small number of balls, most in urn A
Snapshot 6: a small number of balls, most in urn A, after about 50 transfers
Snapshot 7: the same number of balls in both urns
Snapshot 8: the same number of balls in both urns, after about 300 transfers
To play the game, enter the total number of balls and the initial distribution of balls in one of the urns (thus defining the number in the other). The momentary state of each urn is shown graphically and expressed numerically in terms of the absolute number of balls and the percentage of the total number. The system’s evolution is also displayed as a plot of the percentage of balls in each urn versus the transfer index, which represents time (in arbitrary units).
Click the green "start" buttton to begin the random transfer of balls. Click the red "stop" button to pause the transfers. Click the blue "reset" button to restore the initial distribution of the balls prior to the last start. Moving either the "total balls" or "initial number of balls in urn A" slider while the game is running has the same effect as clicking the "reset" button.
When a ball is selected for transfer, it is momentarily shaded and swapped with the topmost ball and then moved to the other urn. You can change the rate of transfer using the "delay" slider.
References
[1] H. C. von Baeyer, Warmth Disperses and Time Passes, New York: The Modern Library, 1999.
[2] Encyclopedia Britannica. "Probability Theory: The Ehrenfest Model of Diffusion." www.britannica.com/EBchecked/topic/477530/probability-theory/32793/The-Ehrenfest-model-of-diffusion.
Permanent Citation
"Ehrenfest's Double-Urn Game"
http://demonstrations.wolfram.com/EhrenfestsDoubleUrnGame/
Wolfram Demonstrations Project
Published: September 2 2014