Eigenfunctions and Energies for Sloped-Bottom Square-Well Potential

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
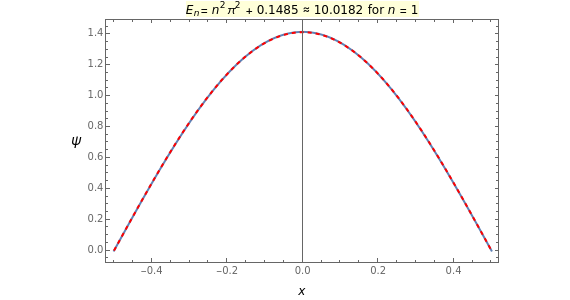
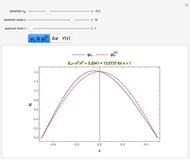
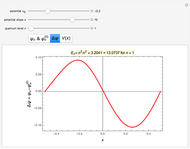
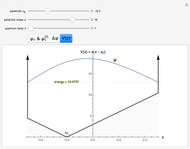
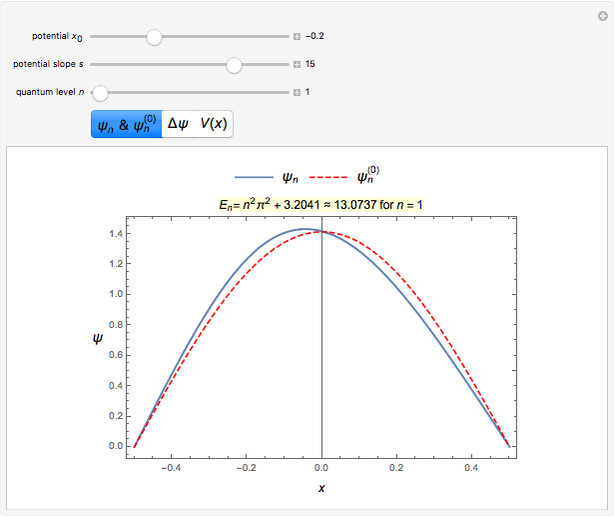
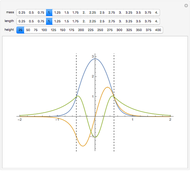
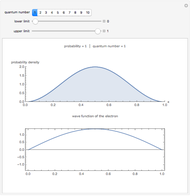
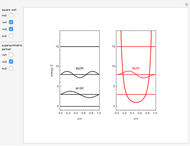
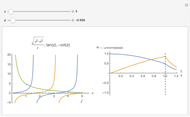
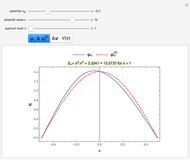
Eigenenergies 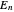 and eigenfunctions
and eigenfunctions 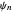 of the potential
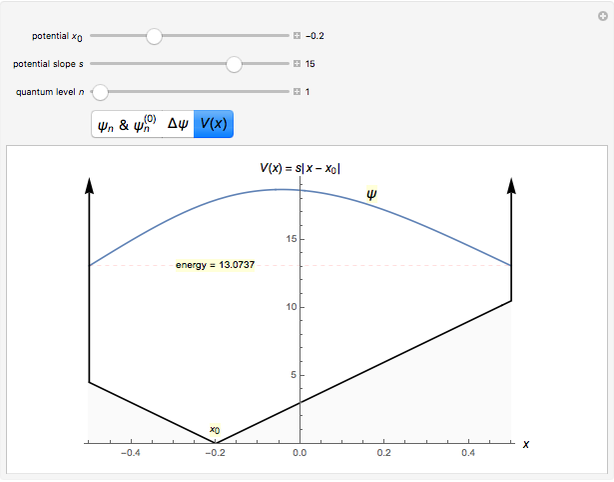
of the potential 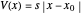 for
for  and
and 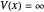 for
for  are obtained numerically. This is treated as a perturbation of the infinite square-well potential, with
are obtained numerically. This is treated as a perturbation of the infinite square-well potential, with 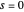 ,
,  for
for 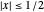 and
and 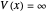 for
for 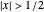 . The
. The  eigenfunction of the unperturbed problem is denoted by
eigenfunction of the unperturbed problem is denoted by  . Note that, for increasing quantum number
. Note that, for increasing quantum number  , the effect of the perturbation diminishes.
, the effect of the perturbation diminishes.
Contributed by: Santos Bravo Yuste (February 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
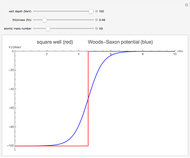
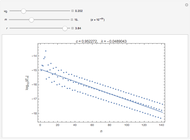
Energies are in units with 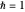 , and the mass of the particle is 1/2. The eigenenergies of the unperturbed potential (the infinite square well of width 1) are
, and the mass of the particle is 1/2. The eigenenergies of the unperturbed potential (the infinite square well of width 1) are 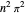 . The case with
. The case with 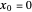 and
and 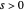 is the "V-bottom" potential, which is studied by perturbation methods in Appendix J of [1]. The case with
is the "V-bottom" potential, which is studied by perturbation methods in Appendix J of [1]. The case with 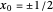 leads to the so-called infinite tilted well. Its exact solution is given in [2].
leads to the so-called infinite tilted well. Its exact solution is given in [2].
References
[1] R. Eisberg and R. Resnick, Quantum Physics of Atoms, Molecules, Solids, Nuclei, and Particles, 2nd ed., New York: Wiley, 1985.
[2] J. N. Churchill and F. O. Arntz, "The Infinite Tilted-Well: An Example of Elementary Quantum Mechanics with Applications toward Current Research," American Journal of Physics, 37(7), 1969 pp. 693–697. doi:10.1119/1.1975775.
Permanent Citation