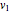Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Elastic Collisions in Galilean Relativity

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

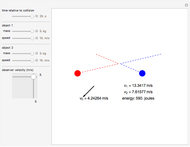
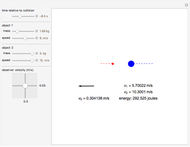
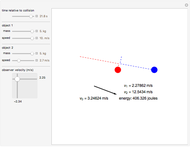
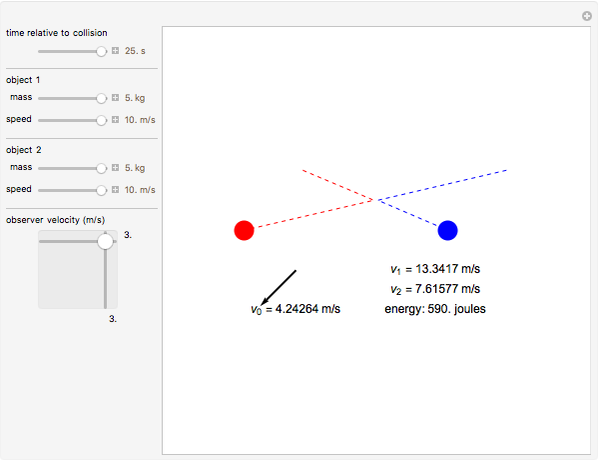
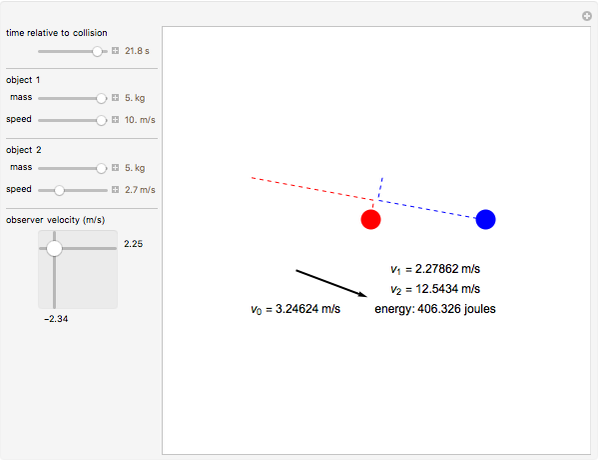
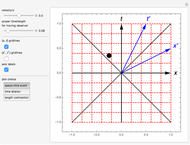
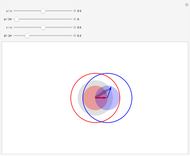
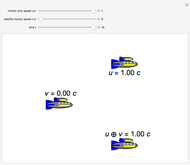
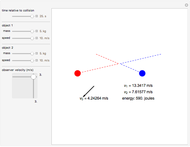
According to the principle of relativity, observers in inertial frames, moving at constant velocities relative to a fixed frame of reference, will experience the same laws of physics, although with different values of observables. In this Demonstration, we consider an observer moving at velocity 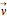relative to the center of mass of two particles undergoing an elastic collision. Different observers will disagree on the magnitudes of momenta and kinetic energy of the system, but they both will agree on the conservation of momentum and energy.

[more]

This Demonstration is based on Galilean relativity, which is an approximation to Einstein's special relativity, accurate only at speeds far slower than the speed of light. You can select the masses and of the two particles and their initial speeds and , as well as two components of the observer's velocity . This velocity vector is shown, along with the speed . The speeds and and the total kinetic energy are also shown on the graphic.

[less]

Contributed by: Joseph Geipel (June 2016)
Open content licensed under CC BY-NC-SA

Snapshots

Details

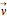The momentum of an object is a vector quantity defined as for the object's mass and vector velocity . The kinetic energy of an object is a scalar quantity defined as 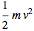, where is the speed. Both of these values, although they might vary from observer to observer, are seen as conserved in an elastic collision. Note that if other forces such as gravity or electromagnetism were acting on the system, the kinetic energy by itself would not be conserved, but, rather, the total energy of the system.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send