Electric Dance: A Symmetrical Three-Body Coulombian System

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
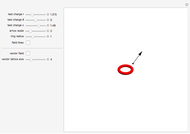
This Demonstration considers a three-body Coulombian system with high symmetry.
[more]
Contributed by: Luca Moroni (January 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
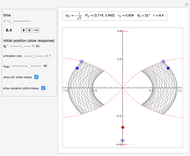
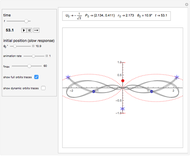
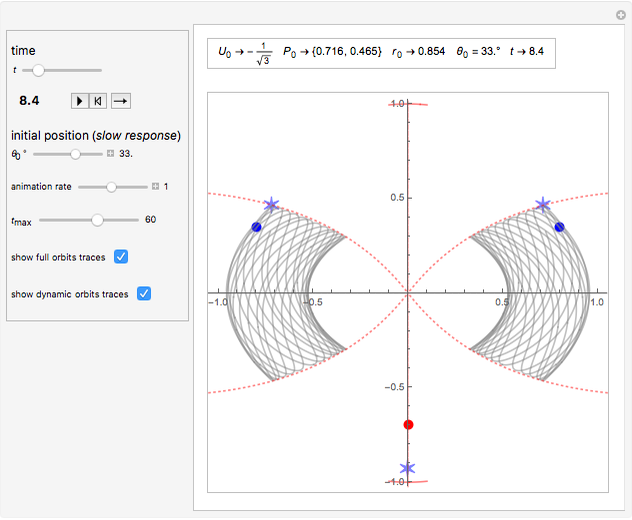
In this Demonstration, the initial position of the rightmost charge is determined just by its angular position 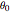 with respect to the origin. Given the fixed initial energy
with respect to the origin. Given the fixed initial energy 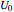 of the system and
of the system and 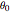 , the radial position is set by the formula:
, the radial position is set by the formula:
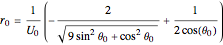 .
.
In Cartesian coordinates, the total potential energy is given by
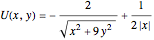 .
.
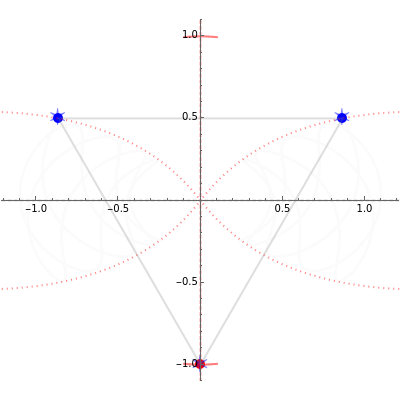
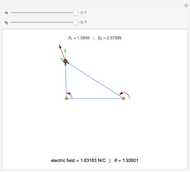
Initially, the three charges form an equilateral triangle inscribed in an unitary circle, and with unitary charges, masses and electric constant 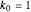 , it is
, it is
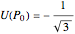 ,
,
where  is the initial position of the right-hand particle.
is the initial position of the right-hand particle.
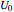 is fixed because this factor only changes the scaling of the orbits and not their qualitative shapes. The positions of the other two charges are determined by the position of the first one, since the three must always form an isosceles triangle with the
is fixed because this factor only changes the scaling of the orbits and not their qualitative shapes. The positions of the other two charges are determined by the position of the first one, since the three must always form an isosceles triangle with the  axis as the axis of symmetry and with the center of mass at the origin.
axis as the axis of symmetry and with the center of mass at the origin.
The evolution of the system is then governed by the Coulomb forces acting on the right-hand particle, due to the presence of the other two particles.
Since the Coulomb force is conservative, the total energy 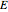 is conserved:
is conserved:
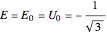 .
.
(The charges have zero kinetic energy at  .) A negative initial energy ensures that the system is bound and that the charges will never escape to infinity.
.) A negative initial energy ensures that the system is bound and that the charges will never escape to infinity.
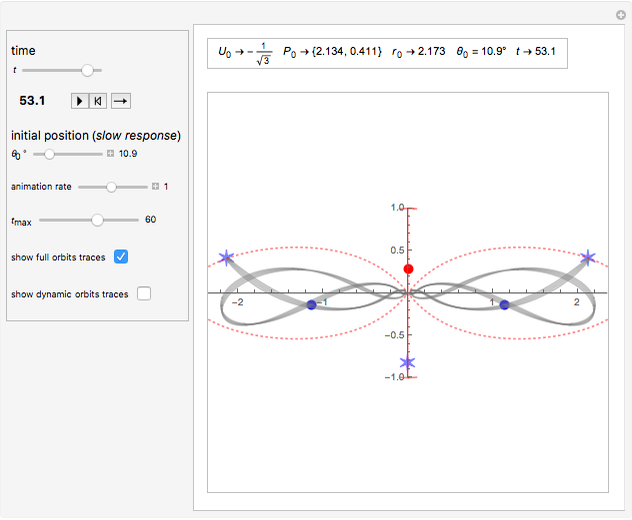
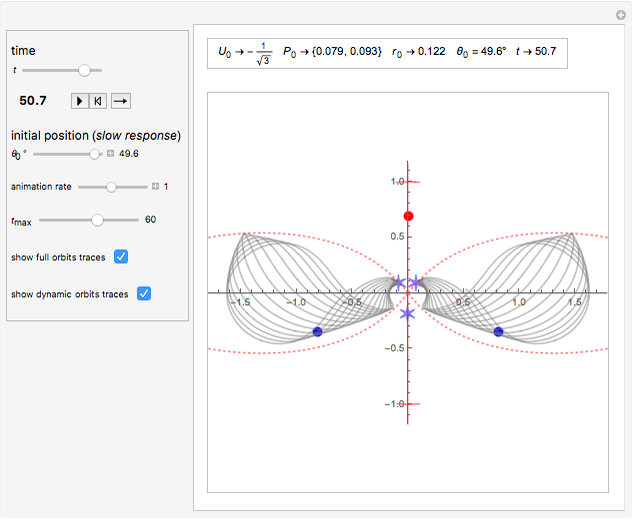
The lines with constant potential 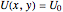 are shown as dotted lines and delimit the region where the blue particles can move. At these lines, a particle has zero speed.
are shown as dotted lines and delimit the region where the blue particles can move. At these lines, a particle has zero speed.
The purpose of this Demonstration is to explore the different kinds of trajectories that this system can produce with different initial conditions; that is, with different isosceles triangles, by changing the parameter 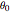 . Some trajectories look periodic and some look quasiperiodic. For instance, the equilateral triangle setting appears to produce a periodic orbit (with a period of about 39.1 s).
. Some trajectories look periodic and some look quasiperiodic. For instance, the equilateral triangle setting appears to produce a periodic orbit (with a period of about 39.1 s).
References
[1] S. Strogatz, Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering, Reading, MA: Addison-Wesley Pub., 1994.
[2] Wikipedia. "Coulomb's Law." (Jan 4, 2017) en.wikipedia.org/wiki/Coulomb's_law.
[3] L. Moroni, "Electric Dance," Worlds of Math & Physics (blog). (Jan 4, 2017) www.lucamoroni.it/electric-dance-page.
[4] L. Moroni, "Electric Dance,"YouTube video" (Jan 4, 2017) https://youtu.be/nqAcMm2o-kk
Permanent Citation