Electromagnetic Waves from a Linear Antenna

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
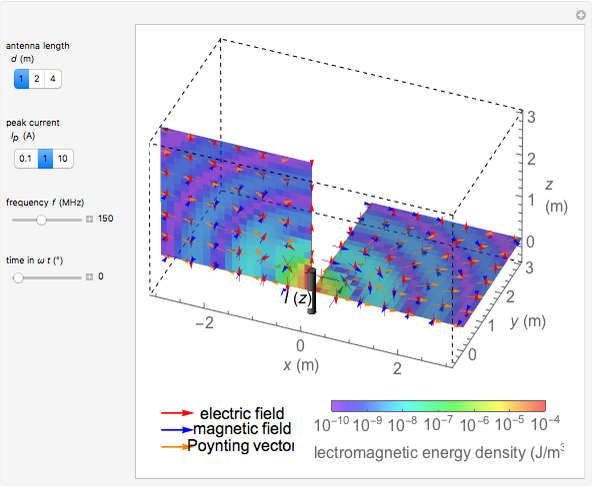
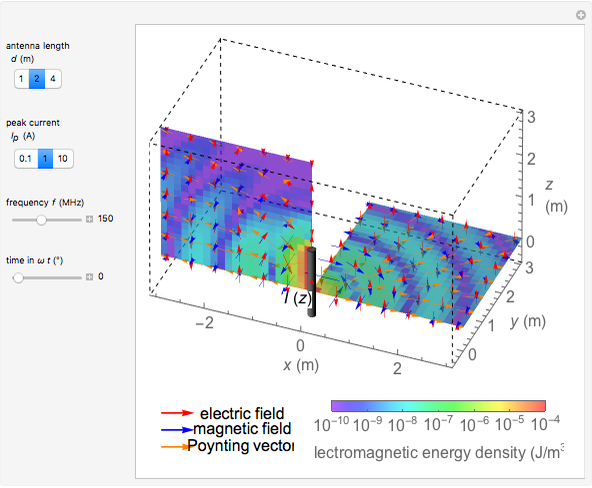
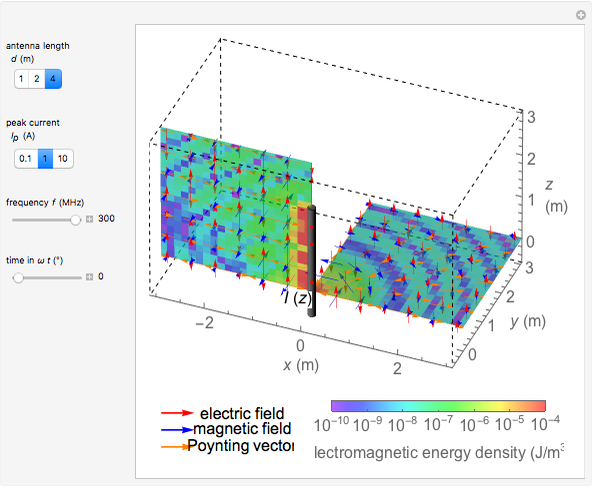
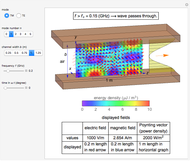
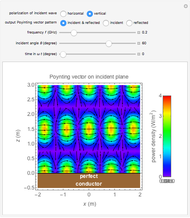
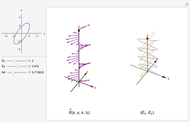
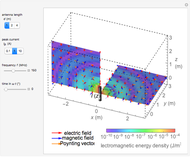
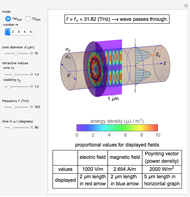
This Demonstration shows the electromagnetic fields around a linear antenna excited by a sinusoidal standing wave. The antenna direction is taken as the  axis. The electric and magnetic fields are displayed in the
axis. The electric and magnetic fields are displayed in the  -
-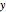 and
and  -
- planes together with Poynting vectors, shown by the arrows with length logarithmically scaled. The electromagnetic energy density is shown by color. You can vary the antenna length
planes together with Poynting vectors, shown by the arrows with length logarithmically scaled. The electromagnetic energy density is shown by color. You can vary the antenna length  , current
, current 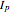 , and frequency
, and frequency  , as well as the observation instant or phase
, as well as the observation instant or phase  . It is possible to see the animation by changing
. It is possible to see the animation by changing  automatically, although you have to reduce the speed to a very low level.
automatically, although you have to reduce the speed to a very low level.
Contributed by: Y. Shibuya (October 2013)
Open content licensed under CC BY-NC-SA
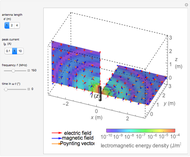
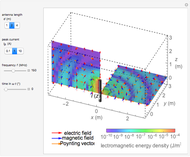
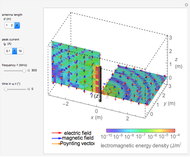
Snapshots
Details
The antenna current is assumed to be a standing wave  , where
, where  is the propagation constant (
is the propagation constant (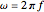 is the angular velocity and
is the angular velocity and  is the speed of light). From the charge conservation law, the charge density per unit length is
is the speed of light). From the charge conservation law, the charge density per unit length is  . These complex values represent harmonic quantities. The scalar and vector potentials are determined by
. These complex values represent harmonic quantities. The scalar and vector potentials are determined by
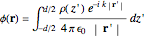 ,
,
 .
.
Using Mathematica's symbolic calculation in vector analysis, it is possible to write down the mathematical equations for the electromagnetic fields 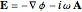 and
and 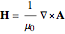 in terms of
in terms of 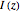 and
and  directly. The somewhat lengthy expressions in the program are derived by approximating the integrations with the summations over the whole length of antenna parts (the number of divisions is set to eight for the sake of simplicity). The instantaneous fields are calculated by
directly. The somewhat lengthy expressions in the program are derived by approximating the integrations with the summations over the whole length of antenna parts (the number of divisions is set to eight for the sake of simplicity). The instantaneous fields are calculated by  and
and  . Correspondingly, the Poynting vector is calculated by
. Correspondingly, the Poynting vector is calculated by  , and the electromagnetic energy density by
, and the electromagnetic energy density by  .
.
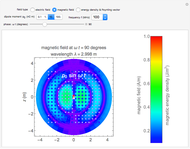
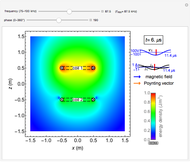
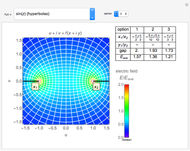
Denoting the wavelength  by
by 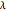 , snapshots 1, 2, and 3 are cases for
, snapshots 1, 2, and 3 are cases for  ,
, 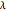 , and
, and  , respectively. In the first two cases, the electromagnetic radiation is directed laterally, but in the relatively long antenna for snapshot 3, substantial radiation is produced near the axial directions.
, respectively. In the first two cases, the electromagnetic radiation is directed laterally, but in the relatively long antenna for snapshot 3, substantial radiation is produced near the axial directions.
Reference
[1] J. D. Jackson, Classical Electrodynamics, 3rd ed., New York: John Wiley & Sons, 1998.
Permanent Citation