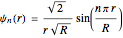Electron in a Nanocrystal Modeled by a Quantum Particle in a Sphere

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
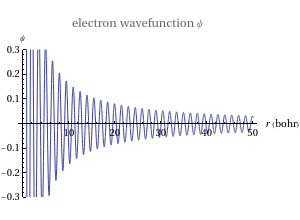
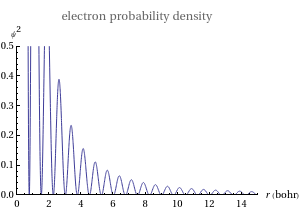
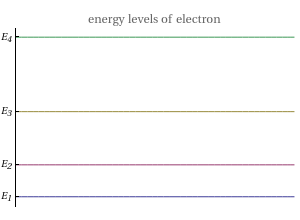
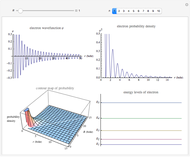
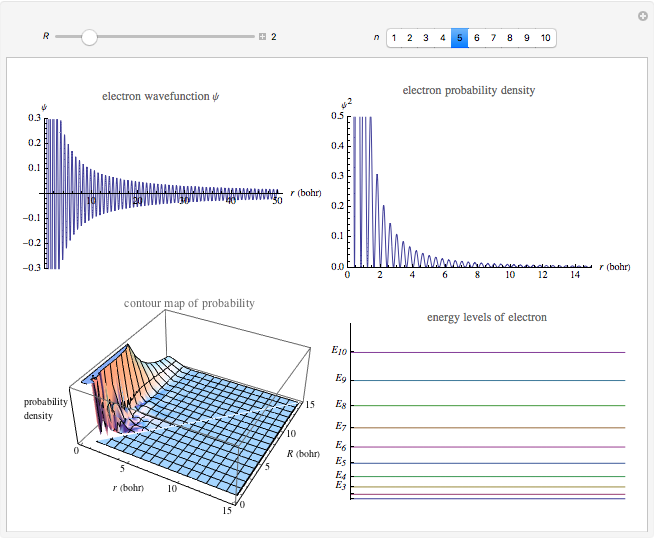
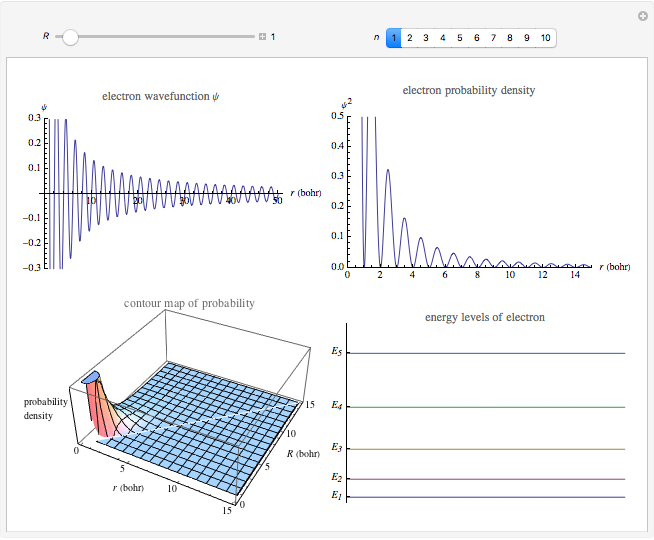
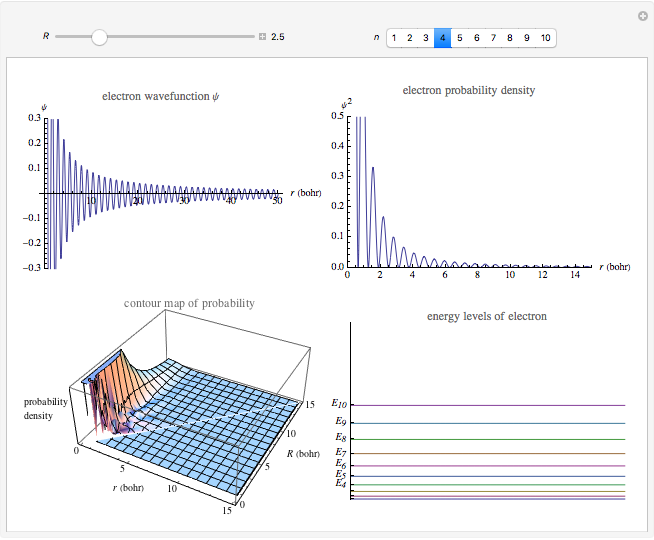
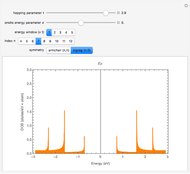
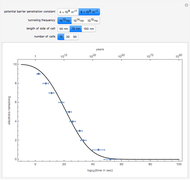
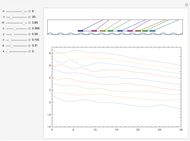
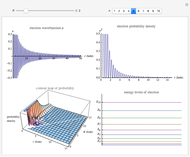
This Demonstration shows the quantum effects observed on a single electron trapped in a spherical nanoparticle (also called a "quantum dot"), modeled as a particle in a sphere. We obtain the relationships among quantum energy levels 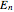 , the radius of the nanoparticle
, the radius of the nanoparticle  , and the distance of the electron from the center of the nanoparticle
, and the distance of the electron from the center of the nanoparticle  by solving the Schrödinger equation. For spherical symmetry, with
by solving the Schrödinger equation. For spherical symmetry, with  and
and  :
:
Contributed by: Yezhi Jin, Kyle Smola, Rahil Ukani (December 2016)
Additional contributions by: Eitan Geva (University of Michigan)
Open content licensed under CC BY-NC-SA
Details
Reference
[1] T. Kippeny, L. A. Swafford and S. J. Rosenthal, "Semiconductor Nanocrystals: A Powerful Visual Aid for Introducing the Particle in a Box," Journal of Chemical Education, 79(9), 2002 pp. 1094–1100. doi:10.1021/ed079p1094.
Submission from the Compute-to-Learn course at the University of Michigan.
Snapshots
Permanent Citation