Electronic Structure of a Single-Walled Carbon Nanotube in Tight-Binding Wannier Representation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
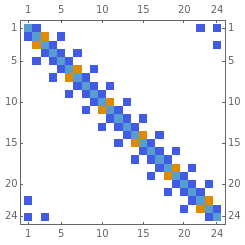
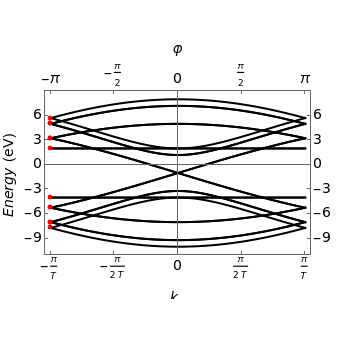
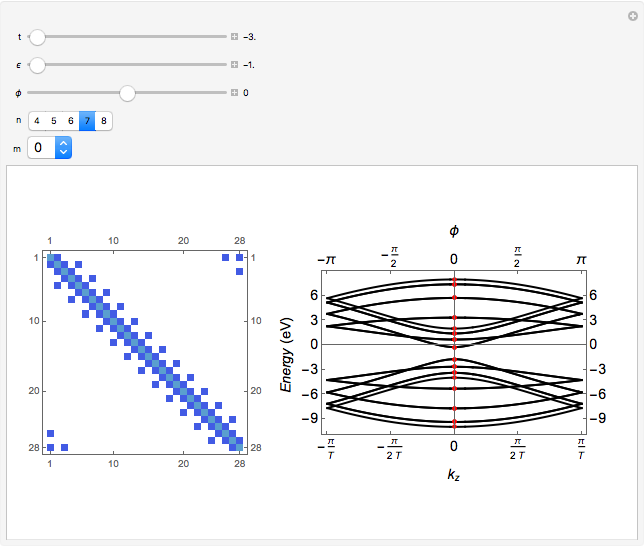
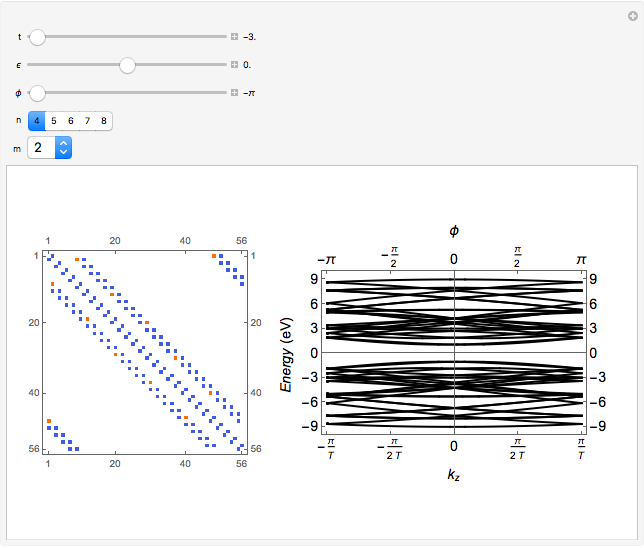
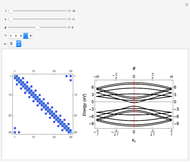
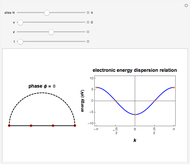
This Demonstration shows an alternative way to represent the reciprocal space zone-folding (ZF) method for computing the tight-binding (TB) electronic structure (right plot) of a single-walled carbon nanotube (SWNT) with given  chirality. The TB Hamiltonian
chirality. The TB Hamiltonian  is constructed in real space representation or Wannier representation and the electronic energy dispersion relation is obtained from the eigenvalues of the corresponding Hamiltonian matrix (left plot). The diagonal matrix elements are given by the on-site energy parameter
is constructed in real space representation or Wannier representation and the electronic energy dispersion relation is obtained from the eigenvalues of the corresponding Hamiltonian matrix (left plot). The diagonal matrix elements are given by the on-site energy parameter  , while the off-diagonal matrix elements are given by the hopping parameter
, while the off-diagonal matrix elements are given by the hopping parameter  . To find which of these matrix elements are nonzero, one has to consider the whole set of the atomic coordinates
. To find which of these matrix elements are nonzero, one has to consider the whole set of the atomic coordinates  in one SWNT unit cell and the hopping of an electron from a given site with coordinates
in one SWNT unit cell and the hopping of an electron from a given site with coordinates  to each of its first three nearest neighbors with coordinates
to each of its first three nearest neighbors with coordinates  . Hence,
. Hence,  for
for  , where
, where  is the carbon-carbon bond length. Periodic boundary conditions along the SWNT axis (for
is the carbon-carbon bond length. Periodic boundary conditions along the SWNT axis (for  with
with  the axial period of the SWNT) can be expressed by multiplying the hopping parameter
the axial period of the SWNT) can be expressed by multiplying the hopping parameter  by the complex exponential phase factor
by the complex exponential phase factor  . By changing the phase
. By changing the phase  in the range
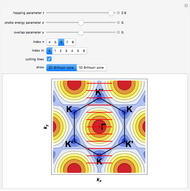
in the range  , the whole 1D Brillouin zone can be sampled. This approach lets you sample a finite number
, the whole 1D Brillouin zone can be sampled. This approach lets you sample a finite number  of Brillouin zone
of Brillouin zone  -points by choosing a finite lattice model with
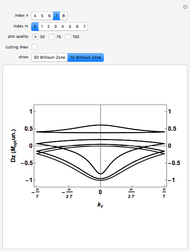
-points by choosing a finite lattice model with  sites; hence the term small crystal approach. In order to show the full equivalence of this method to the reciprocal space zone-folding method, the eigenvalues obtained from diagonalization of the Wannier Hamiltonian
sites; hence the term small crystal approach. In order to show the full equivalence of this method to the reciprocal space zone-folding method, the eigenvalues obtained from diagonalization of the Wannier Hamiltonian  for a given
for a given  are superimposed on the plot of the ZF band structure.
are superimposed on the plot of the ZF band structure.
Contributed by: Jessica Alfonsi (University of Padova, Italy) (January 2010)
Open content licensed under CC BY-NC-SA
Snapshots
Details
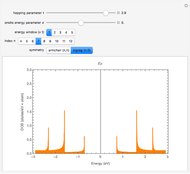
Snapshot 1: electronic structure of a zigzag semiconducting SWNT: 
Snapshot 2: electronic structure of an armchair SWNT (always metallic)
Snapshot 3: electronic structure of a chiral semiconducting SWNT: 
R. Saito, G. Dresselhaus, and M. S. Dresselhaus, Physical Properties of Carbon Nanotubes, London: Imperial College Press, 1998.
J. Alfonsi and M. Meneghetti, "Small Crystal Approach for the Electronic Properties of Double-Wall Carbon Nanotubes," New Journal of Physics, 11, 2009.
J. Alfonsi, "Small Crystal Models for the Electronic Properties of Carbon Nanotubes," PhD thesis, University of Padova, 2009. (chapters 2–4 and references therein)
Permanent Citation