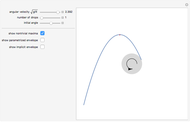
Ellipse Rolling inside a Circle

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
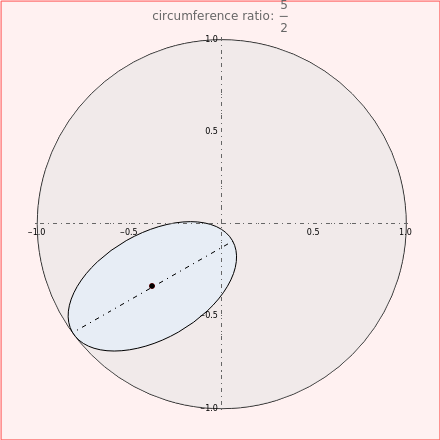
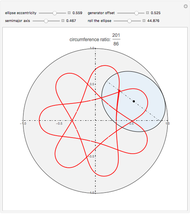
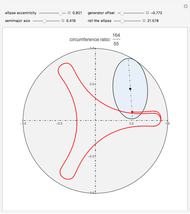
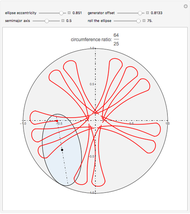
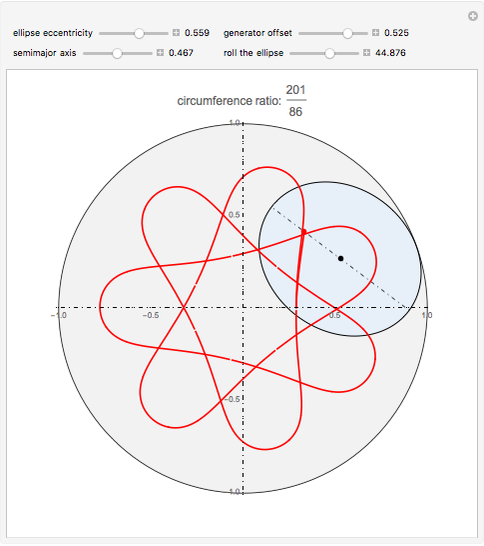
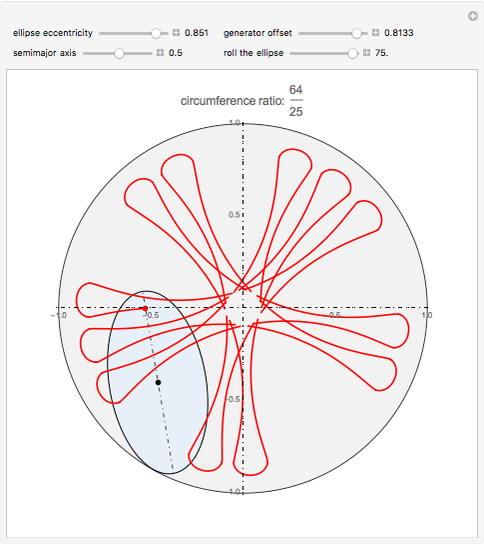
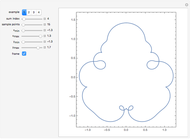
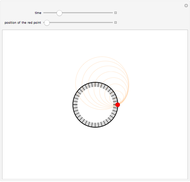
This Demonstration draws the roulette of a generator point on an ellipse that rolls without slipping inside a circle.
[more]
Contributed by: Erik Mahieu (July 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
With the ellipse in its initial position on the right inside the central circle, define two points:
1. The point  on the circle is at an arclength
on the circle is at an arclength  from its intersection with the positive
from its intersection with the positive  axis.
axis.
2. The point  on the ellipse is at an arclength
on the ellipse is at an arclength  from the intersection with its semimajor axis.
from the intersection with its semimajor axis.
Also define two angles:
3.  is the angle subtending an arc of length
is the angle subtending an arc of length  on the circle.
on the circle.
4.  is the angle between the tangent line on the ellipse at
is the angle between the tangent line on the ellipse at  and the
and the  axis.
axis.
Increasing  rolls the ellipse inside the circle by means of two geometric transformations on points
rolls the ellipse inside the circle by means of two geometric transformations on points 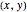 on the ellipse, performed by the Mathematica function transfoEI(ϕ,{x,y},e,a), which consists of a translation by the vector
on the ellipse, performed by the Mathematica function transfoEI(ϕ,{x,y},e,a), which consists of a translation by the vector  and a rotation around
and a rotation around  through the angle
through the angle  .
.
In order for the ellipse to roll inside the central circle, the maximum radius of curvature of the ellipse, 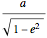 , must be smaller than the radius of the circle, equal to 1. This limits the eccentricity:
, must be smaller than the radius of the circle, equal to 1. This limits the eccentricity: 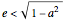 .
.
Permanent Citation