Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Elliptic Curves on a Small Lattice

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

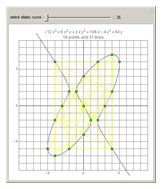
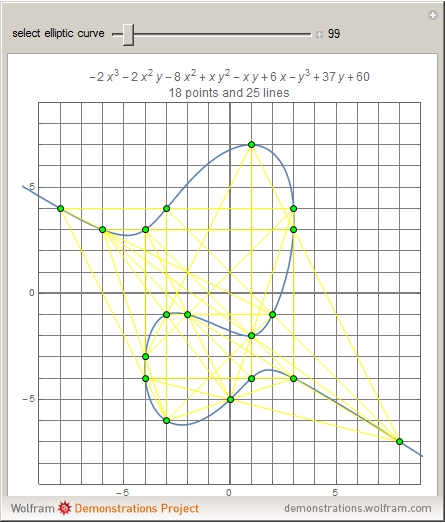
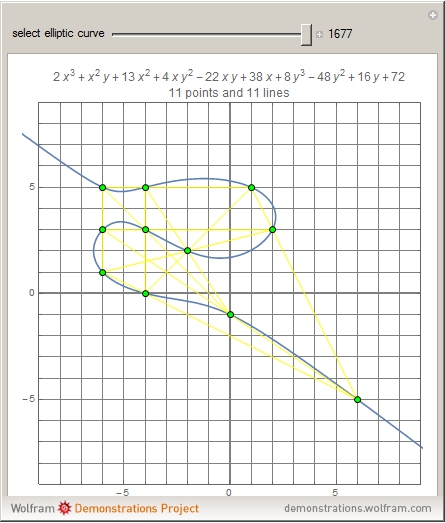
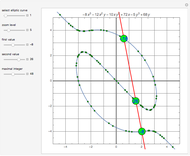
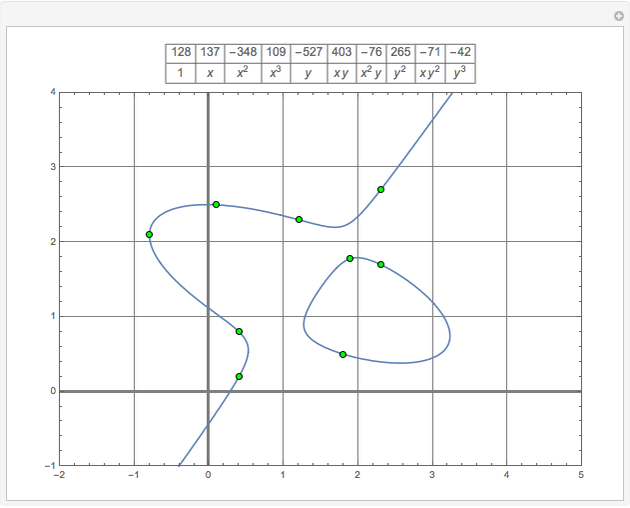
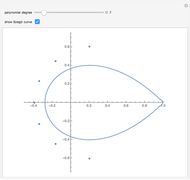
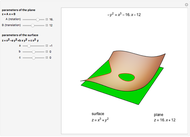
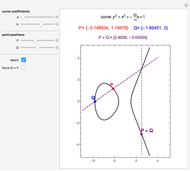
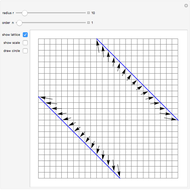
A cubic equation is of the form 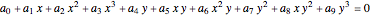. Given any nine lattice points, a cubic equation can be found whose plot, an elliptic curve, goes through all nine points, as shown in the "Nine-Point Cubic" Demonstration. More than nine lattice points can be covered, even when the lattice is tightly restricted.

[more]

If a secant (or nontangent) line is drawn through two rational points on an elliptic curve, it also passes through a third rational point. Integer points are also rational, so it is possible to get a lot of "three-in-a-row" examples with an elliptic curve.

In this Demonstration, more than a thousand elliptic curves were chosen that visit many lattice points; they are roughly ranked by the number of lines they produce.

[less]

Contributed by: Ed Pegg Jr (June 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

detailSectionParagraph
Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send