Elliptic Cylindrical Coordinates

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
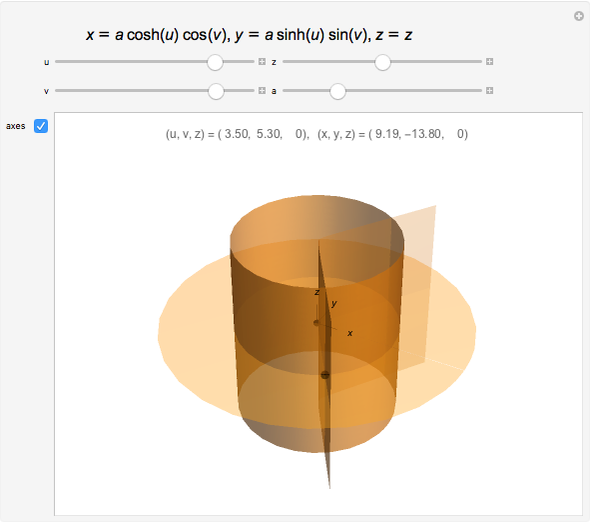
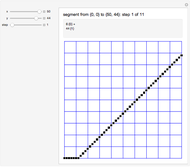
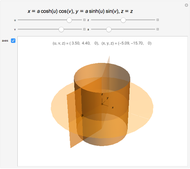
The elliptic cylindrical curvilinear coordinate system is one of the many coordinate systems that make the Laplace and Helmoltz differential equations separable. This system is used when simple boundary conditions on a segment in the  -
- plane are specified, as in the computation of the electric field around an infinite rectangular conducting plate whose intersection with the
plane are specified, as in the computation of the electric field around an infinite rectangular conducting plate whose intersection with the  -
- plane is the line segment with endpoints
plane is the line segment with endpoints  and
and  .
.
Contributed by: Adriano Pascoletti (March 2011)
Open content licensed under CC BY-NC-SA
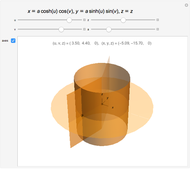
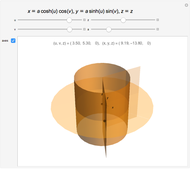
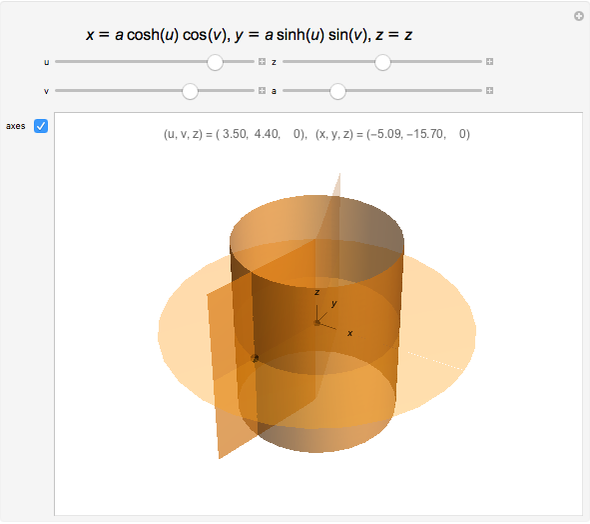
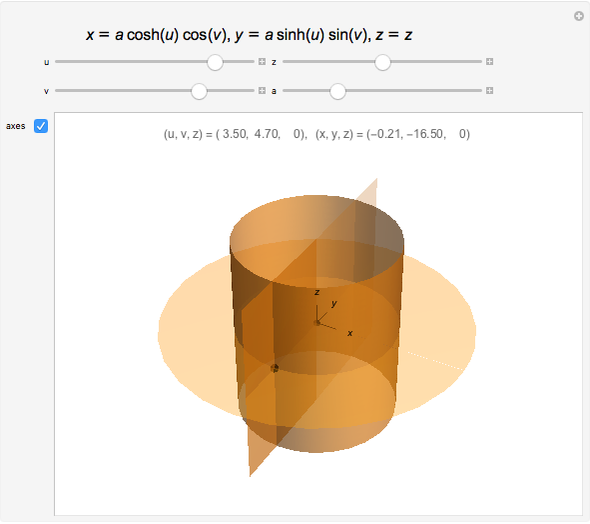
Snapshots
Details
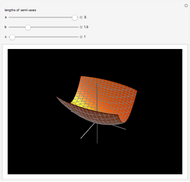
The more opaque half of the hyperbolic cylinder has  ; the other half has
; the other half has  .
.
Permanent Citation