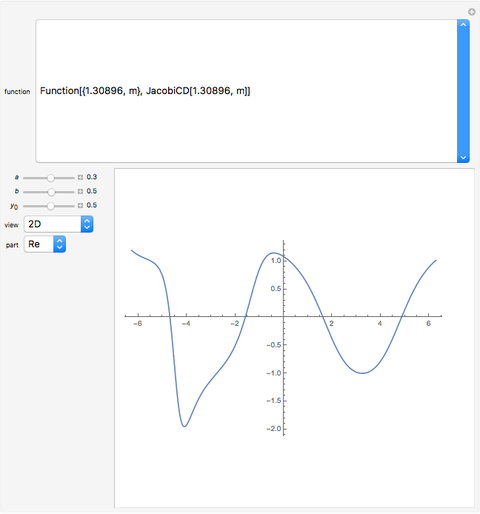
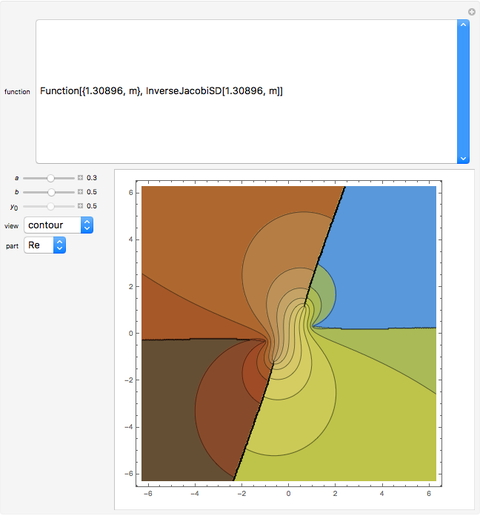
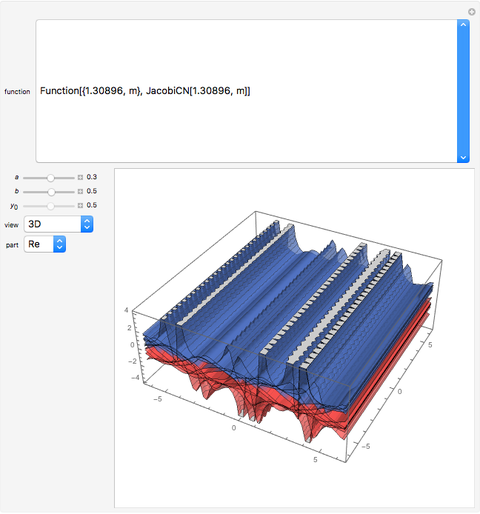
Elliptic Functions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
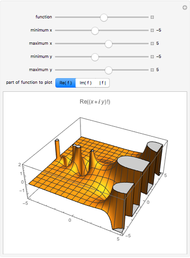
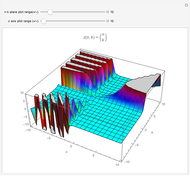
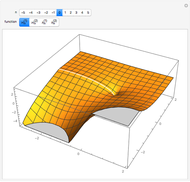
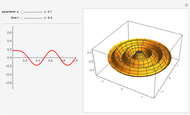
Originally motivated by the computation of the arc length of an ellipse, Jacob Jacobi introduced the theory of Jacobi elliptic functions in the book Fundamenta nova theoriae functionum ellipticarum (New foundations of the theory of the elliptic functions) in 1829. Jacobi elliptic functions are doubly periodic (in the real and imaginary directions) and meromorphic (analytic with the possible exception of isolated poles).
[more]
Contributed by: Enrique Zeleny (November 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Elliptic functions originally arose from the inversion of the integral
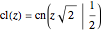 ,
,
known as the incomplete elliptic integral of the first kind, where the angle 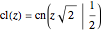 is the amplitude and
is the amplitude and 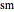 is the modulus. Then define
is the modulus. Then define
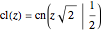 ,
,
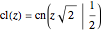 ,
,
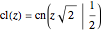 .
.
The reciprocals of the functions 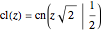 ,
, 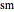 ,
, 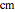 are named by switching the order of the two letters to
are named by switching the order of the two letters to 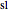 ,
, 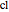 ,
,  ; the ratios of the functions
; the ratios of the functions 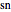 ,
, 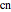 ,
, 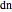 are named by combining the first letters of the functions in the denominator to
are named by combining the first letters of the functions in the denominator to 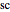 ,
, 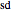 ,
, 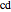 and
and 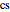 ,
,  ,
, 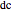 .
.
Also included in this Demonstration are other types of elliptic functions: the Weierstrass elliptic function 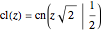 , the Dixon elliptic functions
, the Dixon elliptic functions 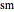 and
and 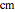 , and the Gauss lemniscate functions
, and the Gauss lemniscate functions 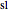 and
and 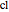 . The Dixon functions and the Weierstrass
. The Dixon functions and the Weierstrass  and the square of its derivative show the symmetries of some of the wallpaper groups. The Dixon functions are defined by
and the square of its derivative show the symmetries of some of the wallpaper groups. The Dixon functions are defined by
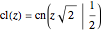 ,
,
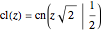 .
.
The Gauss lemniscate functions are defined by
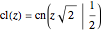 ,
,
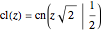 .
.
References
[1] I. S. Gradsteyn and I. M. Ryzhik, Table of Integrals, Series, and Products, 6th ed., San Diego: Academic Press, 2000.
[2] L. M. Milne-Thomson, "Jacobi Elliptic Functions and Theta Functions," in Handbook of Mathematical Functions, (M. Abramowitz and I. A. Stegun, eds.), New York: Dover, 1965.
[3] W. P. Reinhardt and P. L. Walker, "Chapter 22: Jacobian Elliptic Functions," NIST Digital Library of Mathematical Functions, Version 1.0.9; Release date 2014-08-29. dlmf.nist.gov/22.
[4] Souichiro-Ikebe. "Elliptic Functions." Graphics Library of Special Functions (in Japanese). (Dec 4, 2015) http://math-functions-1.watson.jp/sub1_spec_090.html.
[5] A. C. Dixon, The Elementary Properties of the Elliptic Functions, with Examples, London: Macmillan, 1894. archive.org/details/117736039.
[6] A. G. Greenhill, The Applications of Elliptic Functions, London, New York: Macmillan, 1892.
[7] E. T. Whittaker, A Treatise on the Analytical Dynamics of Particles and Rigid Bodies, 4th ed., Cambridge: Cambridge University Press, 1937.
[8] V. G. Tkachev. "Elliptic Functions: Introduction Course." (Nov 7, 2014) www.mai.liu.se/~vlatk48/papers/lect2-agm.pdf.
[9] A. J. Brizard, "A Primer on Elliptic Functions with Applications in Classical Mechanics," arxiv.org/pdf/0711.4064v1.pdf.
[10] Deoxygerbe. "Elliptic Functions on the 17 Wallpaper Groups." Mathematics StackExchange. (May 3, 2011) math.stackexchange.com/questions/36737/elliptic-functions-on-the-17-wallpaper-groups?rq=1.
Permanent Citation
"Elliptic Functions"
http://demonstrations.wolfram.com/EllipticFunctions/
Wolfram Demonstrations Project
Published: November 21 2014