Encoding Structures into Graphs Using Cayley Graphs

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
A set of elements of a group  is said to generate (or to be the generators of)
is said to generate (or to be the generators of)  if the (possibly repeated) application of the generators on themselves and each other is capable of producing all the elements in the group. Given a set of generators (which are obtained by using the built-in Mathematica 8 function GroupGenerators) of
if the (possibly repeated) application of the generators on themselves and each other is capable of producing all the elements in the group. Given a set of generators (which are obtained by using the built-in Mathematica 8 function GroupGenerators) of  , the Cayley graph associated with
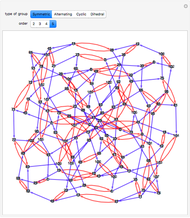
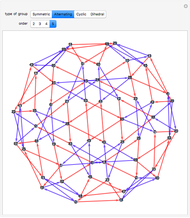
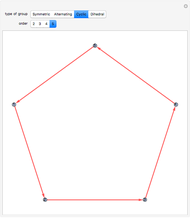
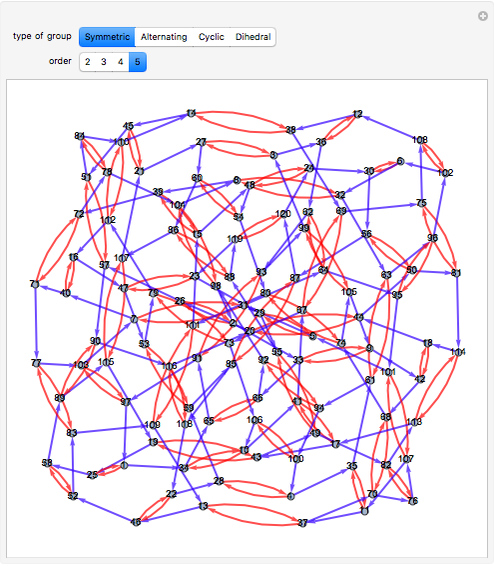
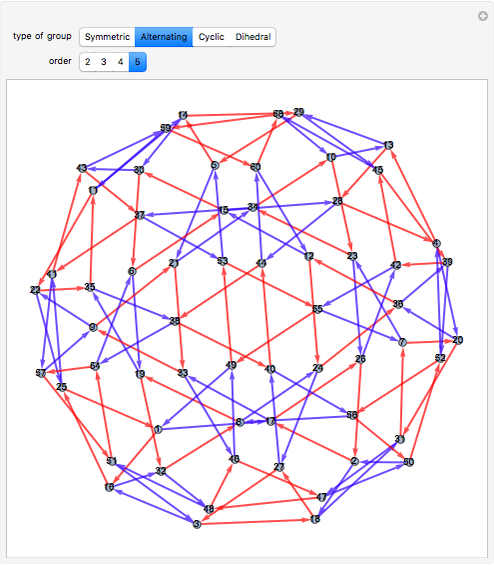
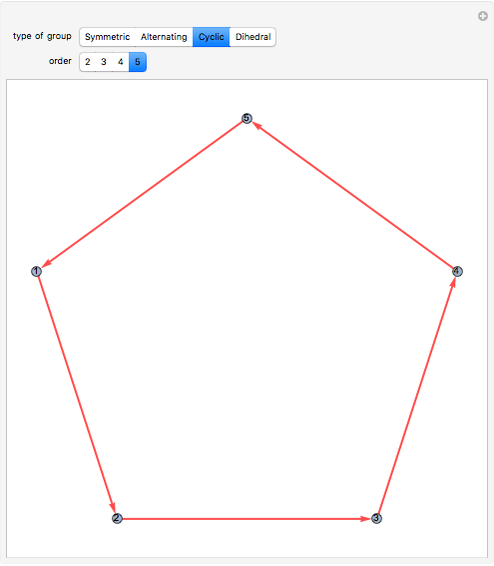
, the Cayley graph associated with  is defined as the directed connected graph having one vertex associated with each group element and directed edges
is defined as the directed connected graph having one vertex associated with each group element and directed edges  whenever
whenever  is a generator. In this Demonstration we construct the Cayley graphs of several types of groups using the CayleyGraph function.
is a generator. In this Demonstration we construct the Cayley graphs of several types of groups using the CayleyGraph function.
Contributed by: Jaime Rangel-Mondragon (August 2011)
Based on work by: Roger Germundsson, Charles Pooh, Jae Bum Jung, Yan Zhuang, Henrik Tidefelt, and Tim Shedelbower
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Encoding Structures into Graphs Using Cayley Graphs"
http://demonstrations.wolfram.com/EncodingStructuresIntoGraphsUsingCayleyGraphs/
Wolfram Demonstrations Project
Published: August 5 2011