Energies for a Heaviside-Lambda Potential Well

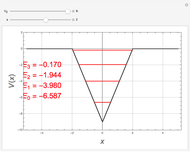
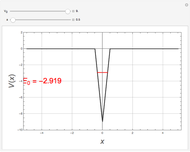
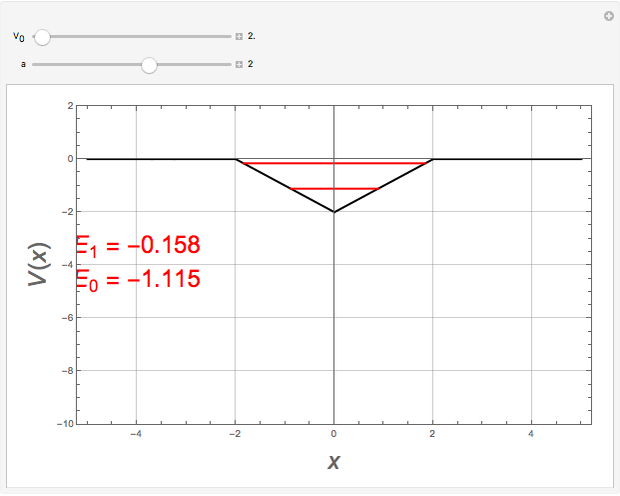
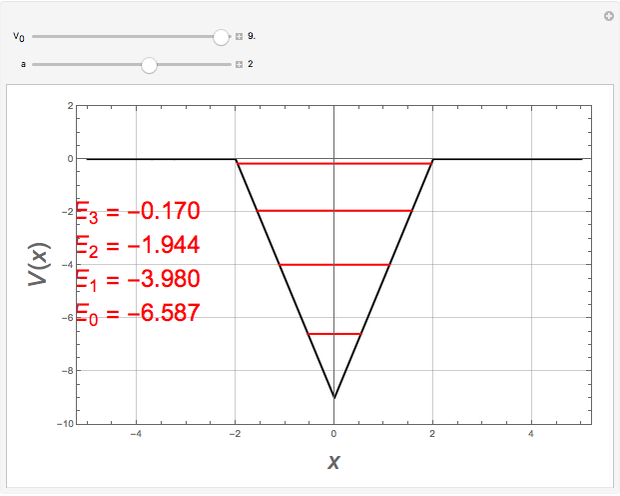
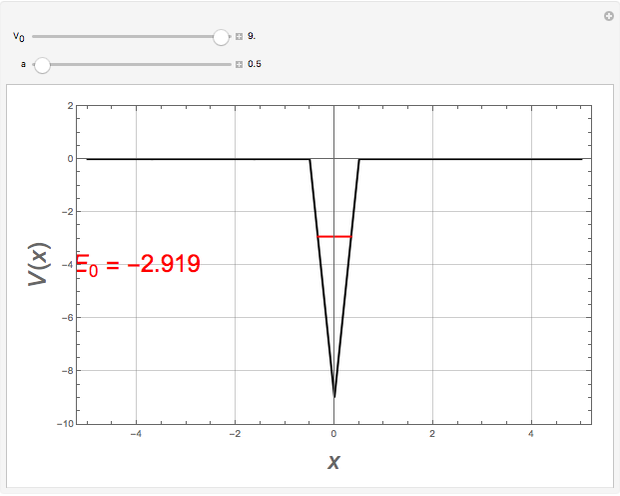
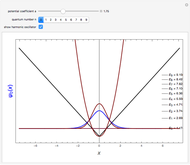
This Demonstration calculates the bound energy levels of a particle in an inverted Heaviside-lambda (vee-shaped) potential well of depth 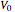and width , using the semiclassical Wentzel–Kramers–Brillouin (WKB) method. The numerical results are within 1% of the values that would be obtained from the exact solutions of the corresponding Schrödinger equation. The energies are determined by the Sommerfeld–Wilson quantization conditions . With 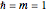, the integral reduces to 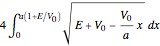, noting that 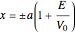are the classical turning points. This can be solved for the energy levels: 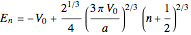, 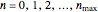. The highest bound state is given by 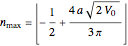, where 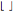is the floor, which for positive numbers is simply the integer part.