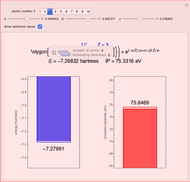
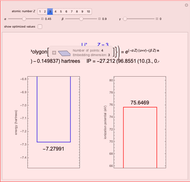
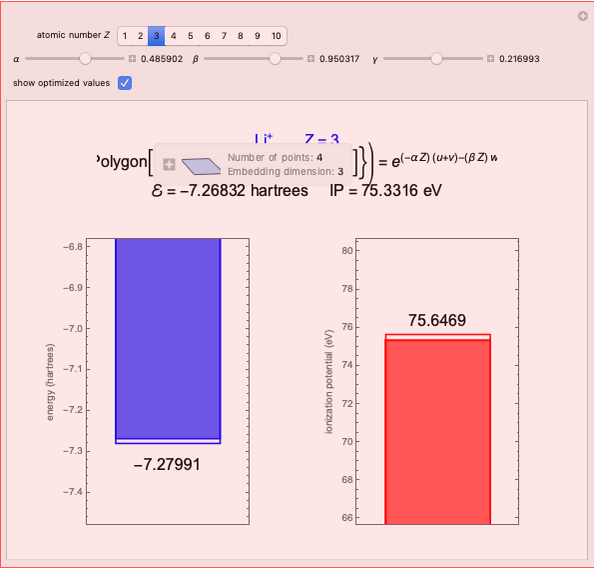
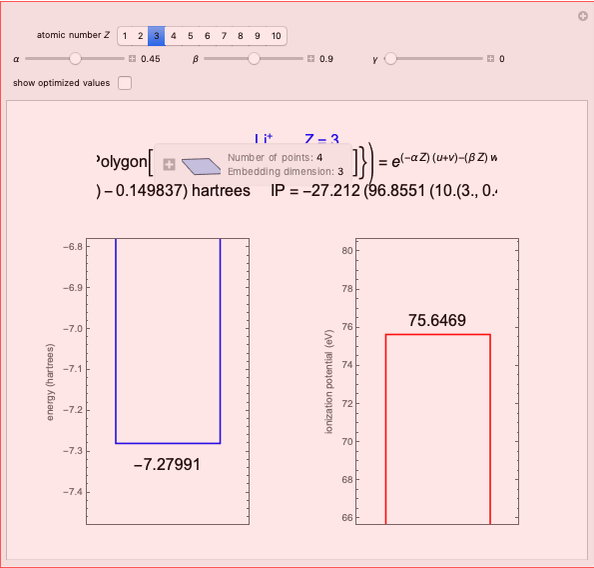
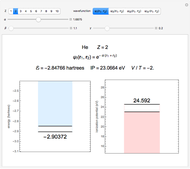
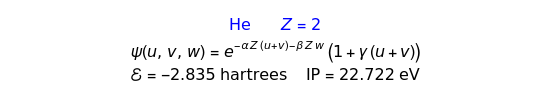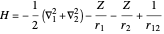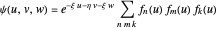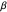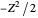Energies of Helium Isoelectronic Series Using Perimetric Coordinates

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
The most accurate computations on the ground state of the helium atom and its isoelectronic series followed from the work of Pekeris [1]. For an S-state, the wavefunction depends on just three coordinates, say  ,
,  and
and  , which can be represented as the sides of a planar triangle. The perimetric coordinates
, which can be represented as the sides of a planar triangle. The perimetric coordinates 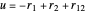 ,
, 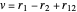 ,
, 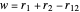 have the advantage that they automatically satisfy the triangle inequalities and each independently varies from 0 to ∞. Pekeris's original computation made use of an expansion in perimetric coordinates containing 1058 terms, leading to the essentially exact nonrelativistic ground-state energy
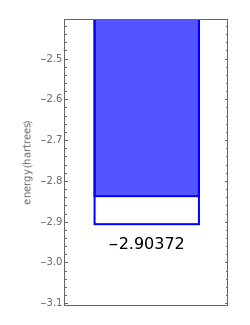
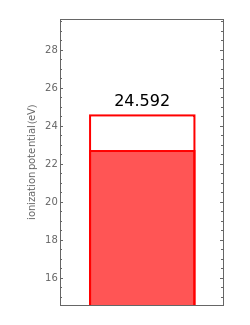
have the advantage that they automatically satisfy the triangle inequalities and each independently varies from 0 to ∞. Pekeris's original computation made use of an expansion in perimetric coordinates containing 1058 terms, leading to the essentially exact nonrelativistic ground-state energy  hartrees. In this Demonstration, we introduce the use of perimetric coordinates in computations on the two-electron isoelectronic series
hartrees. In this Demonstration, we introduce the use of perimetric coordinates in computations on the two-electron isoelectronic series 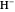 ,
,  ,
, 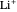 , …,
, …, 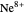 , corresponding to
, corresponding to  in the Hamiltonian
in the Hamiltonian
Contributed by: S. M. Blinder (March 2019)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Perimetric coordinates for two-electron systems:
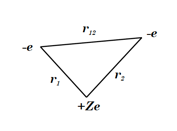
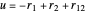 ,
,  ,
,  ,
,
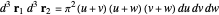 ,
, 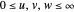 ,
,
 ,
,
 ,
,
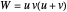 ,
,
 ,
,
 ,
,
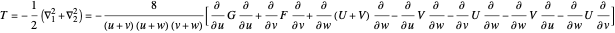 ,
,
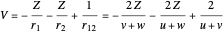 .
.
A more detailed introduction to the quantum theory of two-electron atoms is given in [2].
References
[1] C. L. Pekeris, "Ground State of Two-Electron Atoms," Physical Review, 112(5), 1958 pp. 1649–1658. doi:10.1103/PhysRev.112.1649.
[2] S. M. Blinder, Introduction to Quantum Mechanics in Chemistry, Materials Science, and Biology, Boston: Elsevier, 2004 Chapter 8.
Permanent Citation