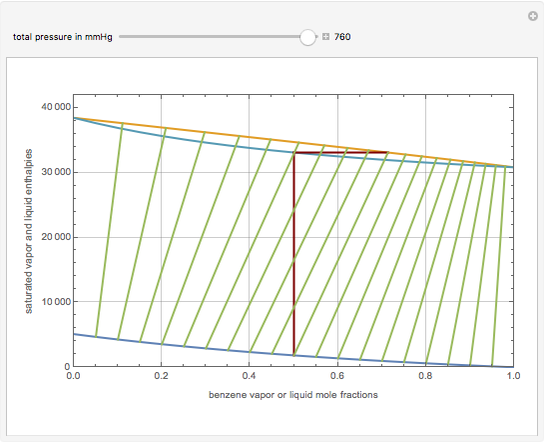
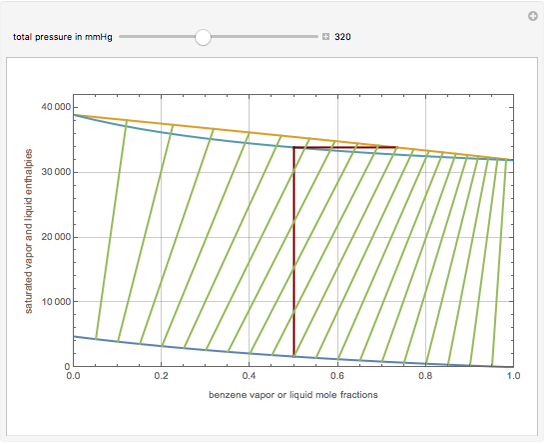
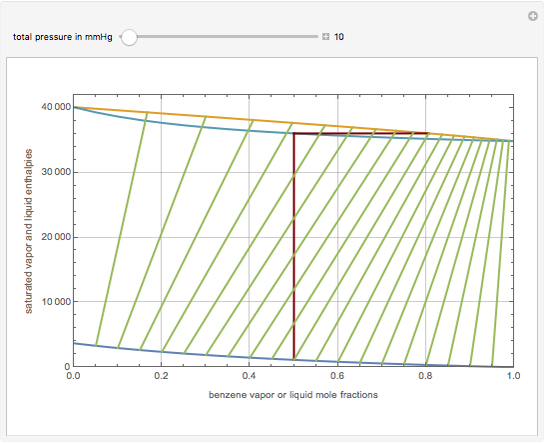
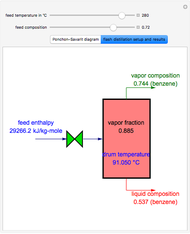
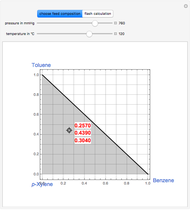
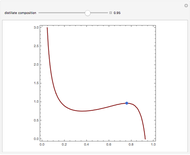
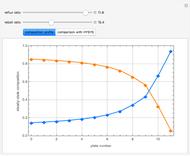
This Demonstration displays the enthalpy-concentration plot for values of the specified total pressure (expressed in mmHg). The ideal binary mixture considered is composed of benzene and toluene. The saturated vapor and liquid enthalpies, 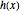and 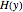(expressed in kJ/kg·mole), are represented by the dark blue and red curves, respectively, where the vapor and liquid mole fractions of benzene are designated by and 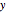, respectively. 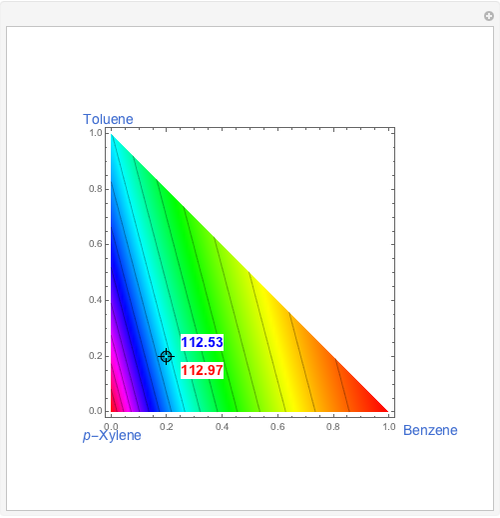The reference temperature, used in the calculation of and , is such that the liquid enthalpy of pure benzene at the boiling point is equal to zero. The tie lines are displayed in green for an equal spacing of the liquid mole fraction of benzene. This Demonstration also shows how any tie line is constructed if the conjugate curve (displayed in light blue) is available. Here, the liquid and vapor enthalpies can be approximated by two parallel lines (i.e., the molar latent heats of chemically similar compounds, benzene and toluene, are almost the same). This has implications in the distillation of the binary benzene-toluene mixture. Indeed, one can safely make the constant molal overflow or CMO assumption, which will result in straight operating lines in the McCabe & Thiele graphical construction.