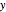Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Envelope Paradox

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

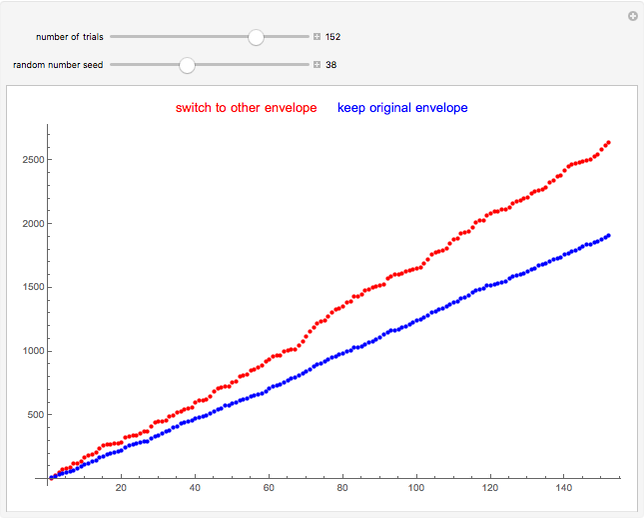
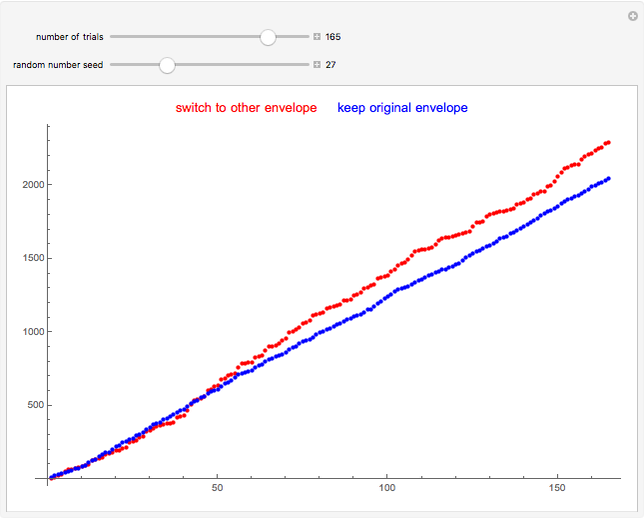
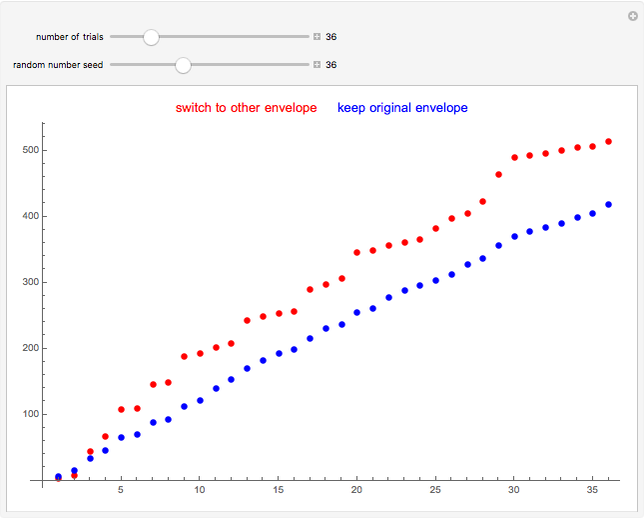
Imagine being presented with two envelopes. The first envelope contains anywhere between $5 to $20, and the other contains either half or double in value. Looking at the first envelope, you are given the option to keep it or switch to the second.

[more]

This problem is known as the exchange paradox. The Demonstration simulates the effectiveness of two different strategies: keeping the first envelope or switching to the second. The red data points represent the strategy of switching to the other envelope, and the blue data points represent keeping the original envelope. The axis is the cumulative amount of money, and the axis is the number of trials.

[less]

Contributed by: Akshay Mishra and Aditya Ponukumati (June 2014)
Open content licensed under CC BY-NC-SA

Snapshots

Details

It is advantageous to choose the envelope with the higher expected value. Assuming a uniform probability density function for the random $5 to $20 amount in the envelope, the expected value can be viewed as the arithmetic mean of all possible envelope values.

Assume the first envelope to enclose an amount , 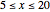. As such, the second envelope either encloses an amoun 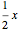or 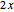. The expected value of this envelope is .

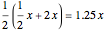Therefore, switching to the second envelope on average nets 25% more money.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send