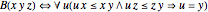Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Equidistance and Betweenness in Euclidean Plane Geometry

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

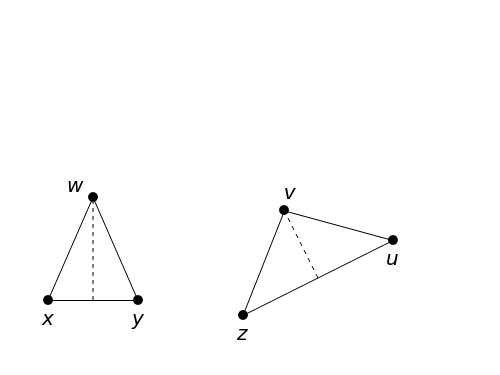
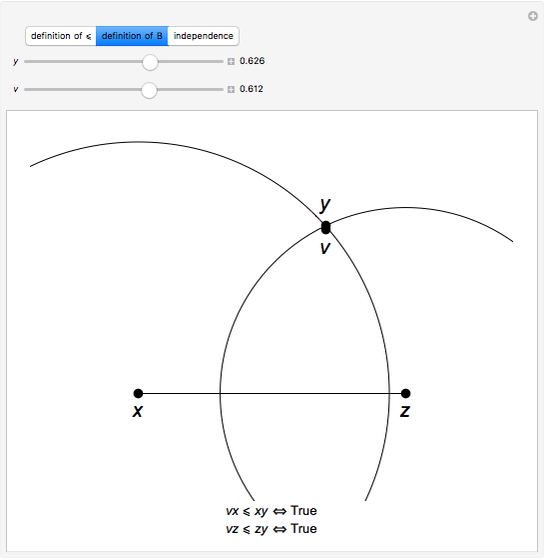
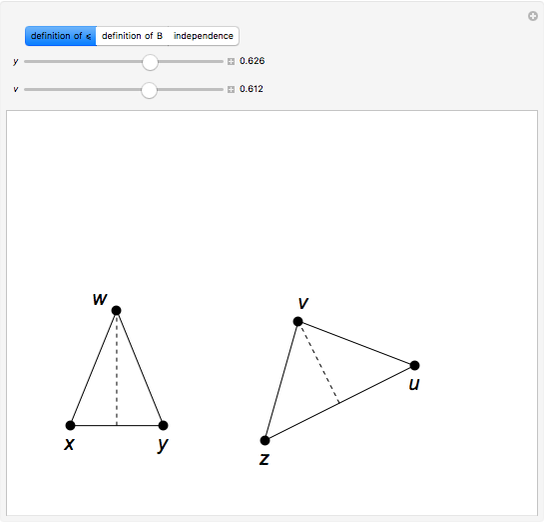
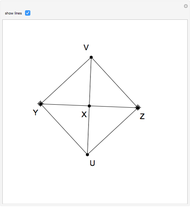
Tarski axiomatized Euclidean plane geometry in first-order logic using two primitive relations: " lies between and ," written as , and " is as distant from as is from ," written as . This Demonstration shows that in plane Euclidean geometry, the relation is definable using relation , but the opposite is not true.

[more]

The first step is to define

.

Using that relation, we define

.

To show that cannot be defined using , two models must be given that preserve the relation but not the relation . The first model is the Cartesian product of real numbers. The second is obtained by using the linear transformation . This transformation preserves lines. We have , but is not true.

[less]

Contributed by: Izidor Hafner (April 2018)
Open content licensed under CC BY-NC-SA

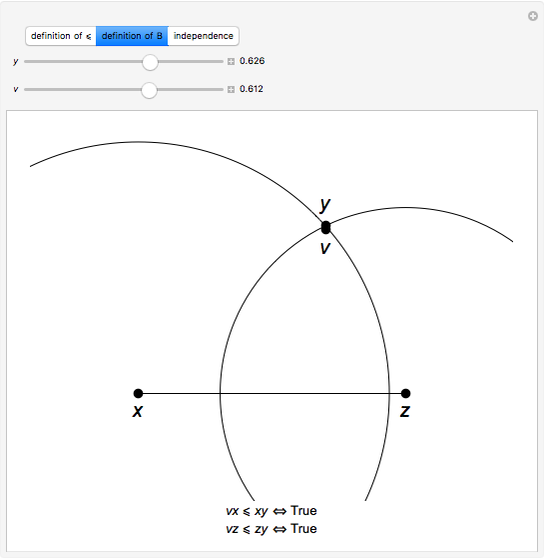
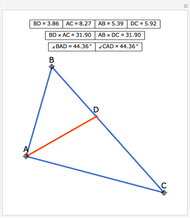
Snapshots

Details

Notation and definitions are from [2].

References

[1] A. Tarski, "What Is Elementary Geography?," The Axiomatic Method: With Special Reference to Geometry and Physics (L. Henkin, P. Suppes and A. Tarski, eds.), Amsterdam: North-Holland, 1959 pp. 16–29.

[2] A. Tarski and S. Givant, "Tarski's System of Geometry," Bulletin of Symbolic Logic, 5(2), 1999 pp. 175–214. www.math.ucla.edu/~asl/bsl/0502/0502-002.ps.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send