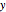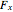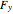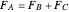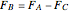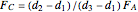Equilibrium of a Rigid Bar
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
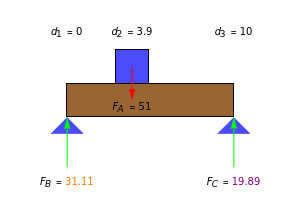
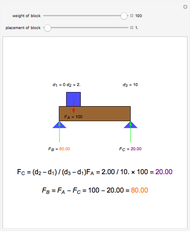
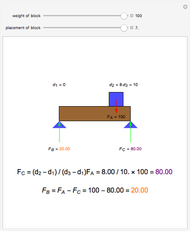
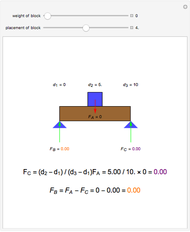
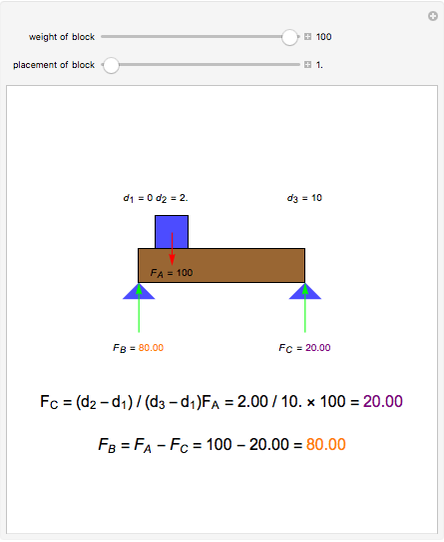
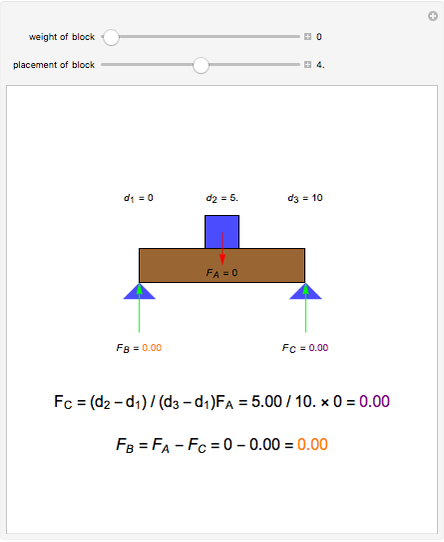
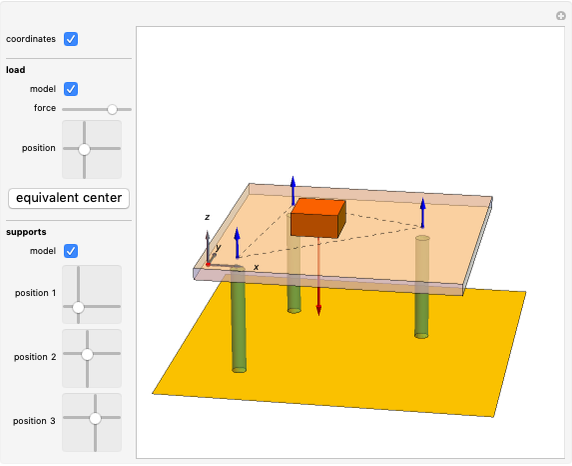
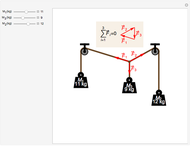
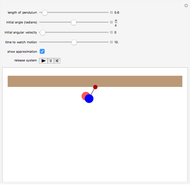
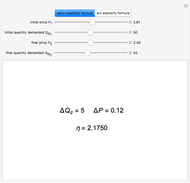
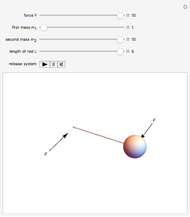
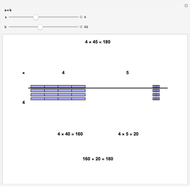
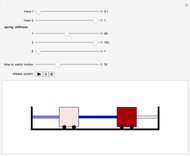
A rigid bar of negligible mass is supported on either end by two triangular blocks. On top of the bar sits a box of variable mass that can be moved along the bar. The forces 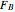 ,
, 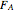 , and
, and 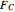 act at
act at 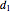 ,
, 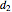 , and
, and 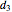 .
.
Contributed by: Sarah Lichtblau (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation