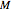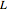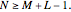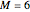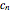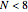Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Equivalence of Linear and Circular Convolutions

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

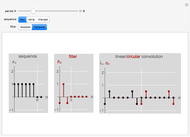
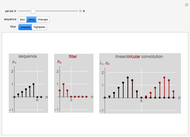
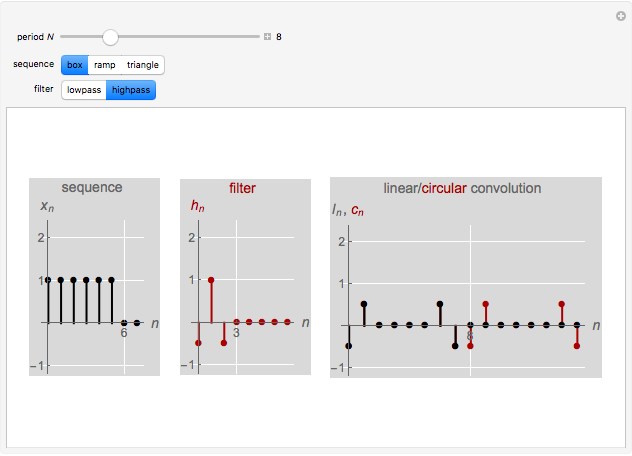
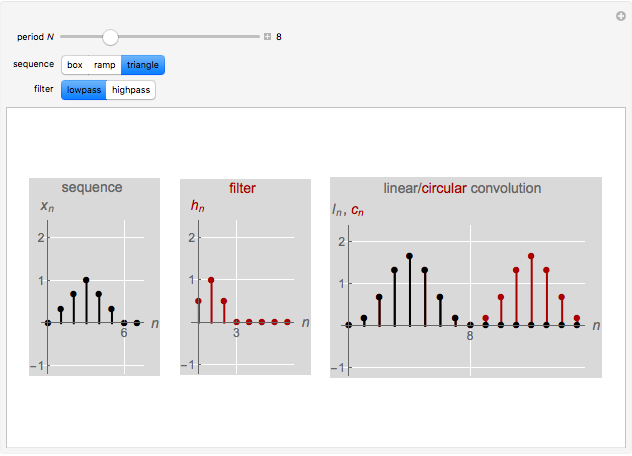
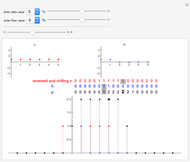
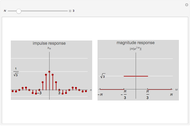
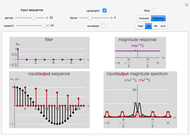
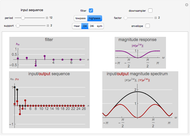
This Demonstration studies the equivalence of linear and circular convolutions. In signal processing, linear convolution (or simply convolution) refers to the convolution between infinitely supported sequences and filters, while circular convolution refers to the convolution between finitely supported and circularly extended sequences and filters (circular extension makes such sequences and filters periodic).

[more]

Given a sequence of length and a filter with an impulse response of length , linear and circular convolutions are equivalent when the period of the circular convolution, , satisfies

In this Demonstration, the first graphic shows the sequence of length , the second graphic shows the filter with impulse response of length , and the third graphic shows the results of linear convolution, (in black), and circular convolution, (in red, repeated with period ). For , linear and circular convolutions are equivalent (black and red stems are identical within one period); for , linear and circular convolutions are not equivalent (black and red stems are not identical within a single period).

[less]

Contributed by: Jelena Kovacevic (July 2012)
Open content licensed under CC BY-NC-SA

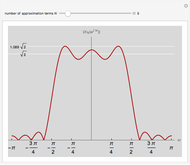
Snapshots

Details

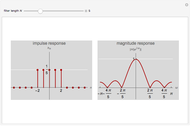
Given a sequence 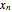and a filter with an impulse response 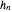, linear convolution is defined as

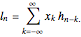
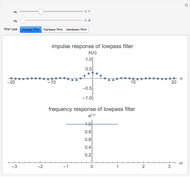
The discrete-time Fourier transform (DTFT) of the linear convolution is the product of the DTFT of the sequence 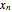and the DTFT of the filter with impulse response 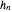; in other words, linear convolution in the time domain is equivalent to multiplication in the frequency (DTFT) domain.

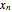Given a length- sequence and a filter with a length- impulse response 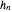, circular convolution is defined by

.

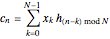The discrete Fourier transform (DFT) of the circular convolution is the product of the DFT of the sequence 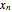and the DFT of the filter with impulse response 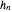; in other words, circular convolution in the time domain becomes multiplication in the frequency (DFT) domain.

Reference

[1] M. Vetterli, J. Kovačević, and V. K. Goyal, Foundations of Signal Processing, Cambridge: Cambridge University Press, 2014. www.fourierandwavelets.org.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send