Equivalential Formula

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
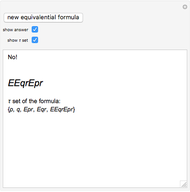
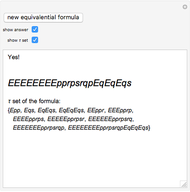
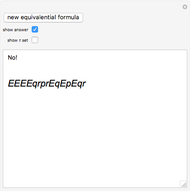
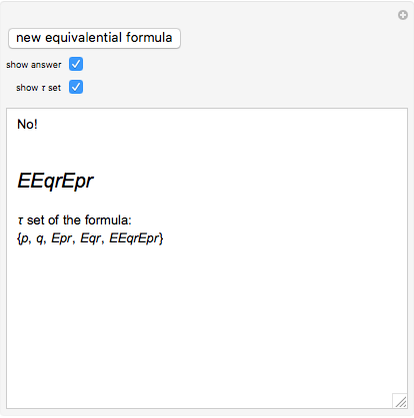
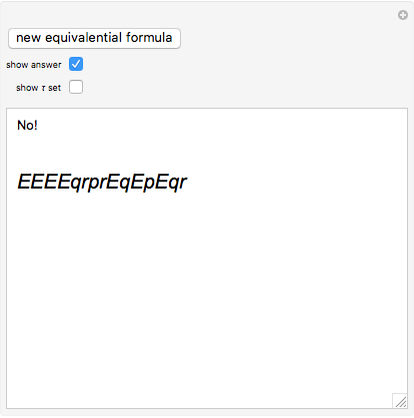
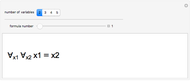
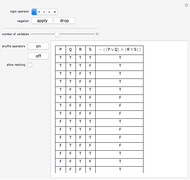
This Demonstration enables the user to decide whether a formula of equivalential calculus is a tautology. Is there any simple rule? The Demonstration also introduces the notion of the 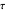 set of a formula, a measure of the symmetry of the formula of equivalential calculus.
set of a formula, a measure of the symmetry of the formula of equivalential calculus.
Contributed by: Izidor Hafner (August 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
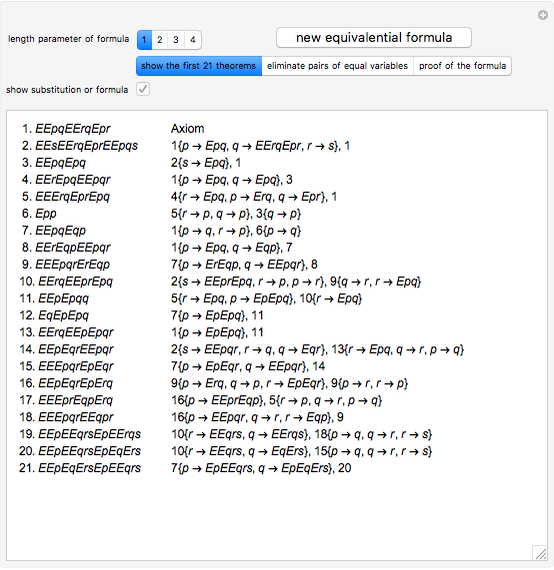
In 1929 Le\:015bniewski recognized that the equivalential calculus could be axiomatized. He also observed that a formula of propositional calculus in which equivalence is the only propositional function is a tautology if and only if each propositional letter occurs an even number of times [1].
The notion of the 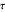 set of a formula of propositional calculus with negation, implication, disjunction and conjunction is introduced in [2].
set of a formula of propositional calculus with negation, implication, disjunction and conjunction is introduced in [2].
The definition for the equivalence is given in [3]:
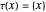 if
if 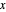 is a propositional variable, otherwise
is a propositional variable, otherwise 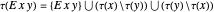 .
.
This definition has a simple consequence for equivalential calculus: a subformula 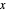 of a formula
of a formula 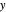 is in
is in 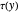 iff there is an odd number of
iff there is an odd number of  occurrences of
occurrences of 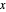 in formula
in formula 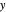 . So
. So 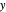 is a tautology iff no propositional variable is in
is a tautology iff no propositional variable is in 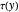 .
.
This notion also gives a linear lower bound on the proof length in equivalential calculus with an axiom schema (where substitution is applicable only to an axiom). We must only construct a set of tautologies with large 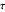 sets.
sets.
The notion also provides a measure for the symmetry of formulas. Only formulas like 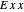 have singleton
have singleton 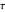 sets.
sets.
References
[1] J. Łukasiewicz, "The Equivalential Calculus," in Polish Logic (1920–1939) (S. McCall, ed.), Oxford: Clarendon Press, 1967, pp. 90–91.
[2] G. S. Ceitin and A. A. Chubaryan, "Some Estimates of Proof Length in Classical Propositional Calculus (in Russian)," Mathematical Questions of Cybernetics and Computation, Erevan, DAN Arm. SSR, 1975 pp. 57–64.
[3] I. Hafner, "On Lower Bound of the Proof Length in the Equivalential Calculus," Glasnik Matematički, 20(40), 1985 pp. 269–270.
Permanent Citation