Erosion Index for Particulates

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
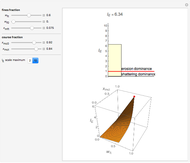
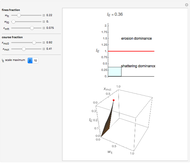
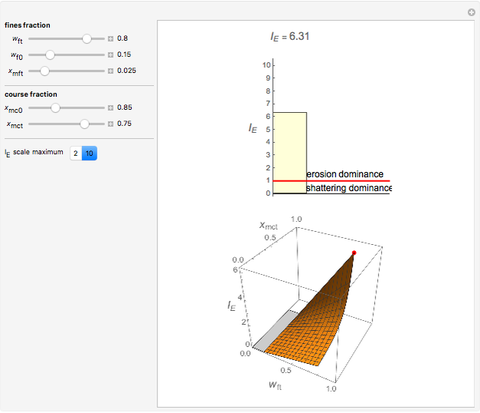
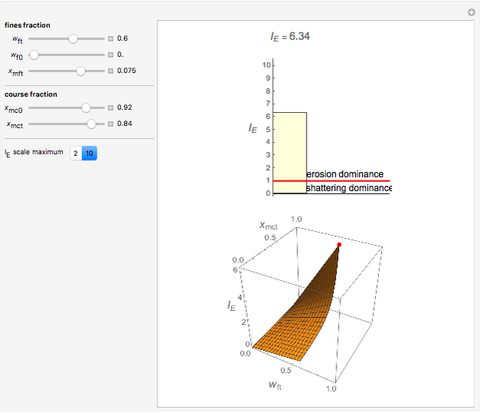
Particulates disintegration, spontaneous or intentionally induced, is frequently the result of shattering and/or surface erosion. The dominance of one mechanism over the other can be characterized by an erosion index,  , computed from the relative size and mass fraction of the fine and coarse particles at any given time. This Demonstration lets you select the fines' initial and momentary mass fractions, and the relative sizes of both the fine and coarse fractions, which are used to calculate and display the erosion index. If
, computed from the relative size and mass fraction of the fine and coarse particles at any given time. This Demonstration lets you select the fines' initial and momentary mass fractions, and the relative sizes of both the fine and coarse fractions, which are used to calculate and display the erosion index. If 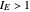 , then there is dominant erosion; if
, then there is dominant erosion; if 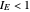 , there is dominant shattering.
, there is dominant shattering.
Contributed by: Mark D. Normand and Micha Peleg (March 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
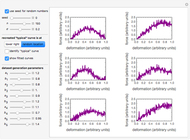
Snapshot 1: instant coffee agglomerates after 15 taps
Snapshot 2: instant coffee agglomerates after 120 taps
Snapshot 3: freeze-dried coffee agglomerates after 180 taps
Snapshot 4: freeze-dried coffee agglomerates after 260 taps
During their transport, handling, and processing, particulates tend to disintegrate by shattering or surface erosion. The result can be size reduction or size reduction accompanied by the formation of fines or dust. In shattering, the daughter particles' size is on the order of half that of the initial, whereas in erosion, the size of the produced fines is much smaller. Thus, in shattering, the particle size is reduced significantly and rapidly. In surface erosion, fines are produced almost exclusively, and therefore the coarse fraction's particle size is little affected. The relative contributions of these two mechanisms can be quantified by an erosion index,  , which is defined as
, which is defined as 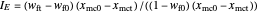 , where
, where  and
and  are the initial and momentary mass fractions of the fines (
are the initial and momentary mass fractions of the fines ( and
and 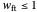 ),
), 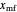 is the dimensionless mode of the fines' size distribution, assumed to be constant, and
is the dimensionless mode of the fines' size distribution, assumed to be constant, and 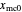 and
and  are the initial and momentary dimensionless modes of the coarse particles' size distribution [1]. If the fines or coarse fraction's size distribution is symmetric, the mode equals the mean particle size.
are the initial and momentary dimensionless modes of the coarse particles' size distribution [1]. If the fines or coarse fraction's size distribution is symmetric, the mode equals the mean particle size.
The formula for calculating 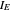 is derived from the ASTM shattering index [2], amended to account for the fines formation and normalizing both fractions' particle sizes [1]. Notice that if the original mass contains no fines (i.e.,
is derived from the ASTM shattering index [2], amended to account for the fines formation and normalizing both fractions' particle sizes [1]. Notice that if the original mass contains no fines (i.e., 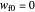 ) and the size of the fines produced is very small relative to that of the coarse particles, then
) and the size of the fines produced is very small relative to that of the coarse particles, then 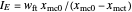 . Either way,
. Either way, 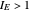 implies dominant erosion and
implies dominant erosion and 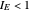 , dominant shattering. Thus, in processes where the mechanisms dominance is reversed, as in erosion turned into shattering (see snapshots 1 and 2),
, dominant shattering. Thus, in processes where the mechanisms dominance is reversed, as in erosion turned into shattering (see snapshots 1 and 2),  will drop from a value greater than one to smaller than one. The opposite will happen if shattering is replaced by erosion.
will drop from a value greater than one to smaller than one. The opposite will happen if shattering is replaced by erosion.
In this Demonstration, you can enter the values of 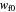 ,
,  ,
, 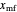 ,
, 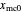 , and
, and 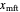 with sliders and the program will compute and display the corresponding
with sliders and the program will compute and display the corresponding 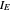 numerically and graphically as a bar chart in 2D and as a red point on a 3D surface plot. You can choose the upper limit of the
numerically and graphically as a bar chart in 2D and as a red point on a 3D surface plot. You can choose the upper limit of the 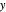 axis in the 2D bar chart with a setter bar for increased resolution.
axis in the 2D bar chart with a setter bar for increased resolution.
References
[1] L. M. Popplewell and M. Peleg, "An 'Erosion Index' to Characterize Fines Production in Size Reduction Processes," Powder Technology, 58(2), 1989 pp.145–148. doi:10.1016/0032-5910(89)80027-0.
[2] Standard Test Method of Drop Shatter Test for Coal, ASTM D440 - 07(2012), ASTM International, West Conshohocken, PA, 2012. doi:10.1520/D0440-07R12.
Permanent Citation