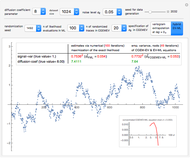
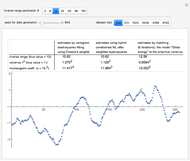
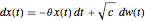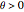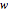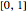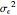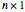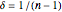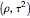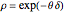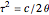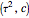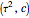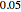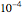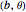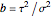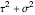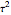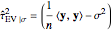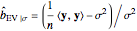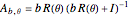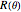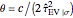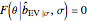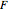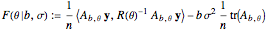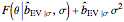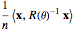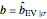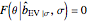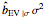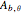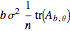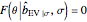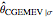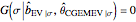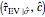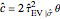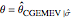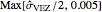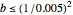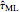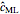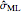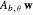Estimators of a Noisy Centered Ornstein-Uhlenbeck Process and Its Noise Variance

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
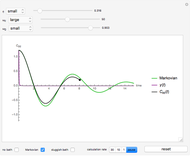
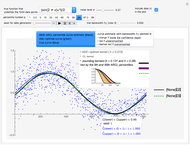
This Demonstration considers three estimators for a noisy centered Ornstein–Uhlenbeck process. This work is a logical sequel to [1]; they both consider a classic "AR1 plus noise" model for time series, but in [1], the noise variance was assumed to be known. Recall the setting and notations in [1]: an underlying process, assumed to be a stationary solution to the differential equation
[more]
Contributed by: Didier A. Girard (October 2018)
(CNRS-LJK and Univ. Grenoble Alpes)
Open content licensed under CC BY-NC-SA
Details
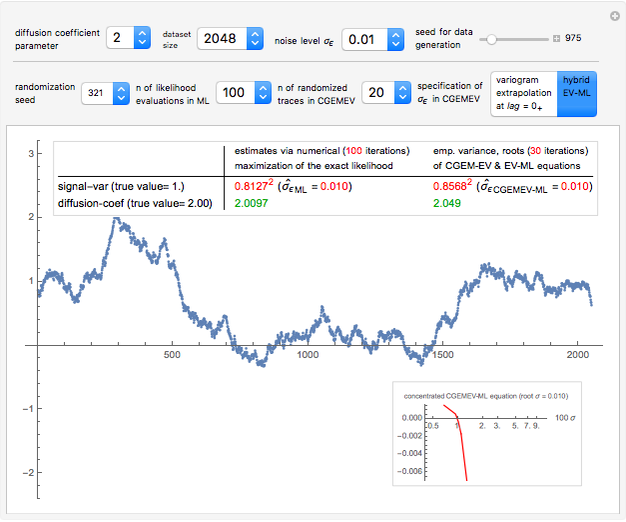
Each realization of the underlying process (a non-noisy dataset) is generated by using the built-in function OrnsteinUhlenbeckProcess. Changing 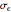 consists of adding a standard Gaussian white noise series that is amplified by the chosen
consists of adding a standard Gaussian white noise series that is amplified by the chosen 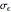 to such a non-noisy dataset.
to such a non-noisy dataset.
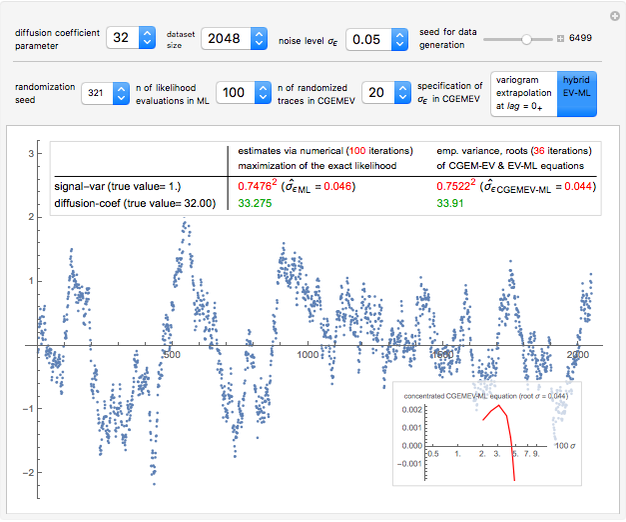
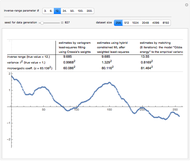
Snapshot 1: Select "diffusion coefficient parameter" 32 (the value of  from which the non-noisy data is simulated),
from which the non-noisy data is simulated),  being fixed, and choose
being fixed, and choose 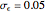 . This setting (with
. This setting (with  ) is also analyzed in Snapshot 1 of [1]. There it was observed that CGEMEV with a priori known
) is also analyzed in Snapshot 1 of [1]. There it was observed that CGEMEV with a priori known 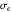 was much more efficient than the neglecting-errors-ML; this holds as long as the noise level stays greater than, say,
was much more efficient than the neglecting-errors-ML; this holds as long as the noise level stays greater than, say, 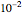 . The two methods—ML taking account of an unknown
. The two methods—ML taking account of an unknown 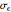 and CGEMEV-ML—have very similar statistical efficiencies.
and CGEMEV-ML—have very similar statistical efficiencies.
The third method, CGEMEV using 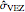 , is obtained by clicking "variogram extrapolation at 0+" instead of "hybrid EV-ML". It is not so bad considering that it is sometimes 10 times faster than CGEMEV-ML. First, as in ML or CGEMEV-ML, a lower bound is imposed on
, is obtained by clicking "variogram extrapolation at 0+" instead of "hybrid EV-ML". It is not so bad considering that it is sometimes 10 times faster than CGEMEV-ML. First, as in ML or CGEMEV-ML, a lower bound is imposed on 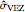 ; precisely
; precisely  is used as soon as
is used as soon as  . By changing the generation-seed, this lower bound is often active when
. By changing the generation-seed, this lower bound is often active when  . This is no longer the case when we come back to
. This is no longer the case when we come back to 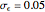 . More precisely, for a seed of 6499, you can see that CGEMEV❘
. More precisely, for a seed of 6499, you can see that CGEMEV❘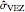 gives a slight underestimation of
gives a slight underestimation of 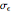 and an overestimation of
and an overestimation of  ; for other seeds, these errors of estimation are in the opposite direction (see, for instance, a seed of 6517). These "small" inaccuracies of the nonparametric
; for other seeds, these errors of estimation are in the opposite direction (see, for instance, a seed of 6517). These "small" inaccuracies of the nonparametric 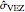 are very often corrected by CGEMEV-ML.
are very often corrected by CGEMEV-ML.
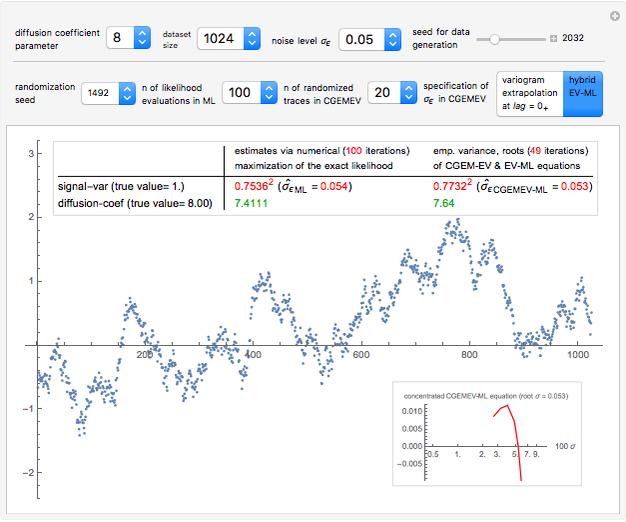
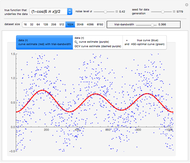
Snapshot 2: Keeping 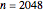 and selecting a small
and selecting a small  (here
(here 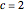 ) as the "diffusion coefficient parameter" (so that we are close to the near unit root situation), a noise with
) as the "diffusion coefficient parameter" (so that we are close to the near unit root situation), a noise with 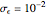 can no longer be considered as a negligible noise. This claim can be easily demonstrated by playing with [1] where "not negligible noise" means that the neglecting-errors-ML method cannot be trusted. The good news is that with such small
can no longer be considered as a negligible noise. This claim can be easily demonstrated by playing with [1] where "not negligible noise" means that the neglecting-errors-ML method cannot be trusted. The good news is that with such small  , the noise level
, the noise level 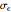 can now be reliably estimated, even when it is only
can now be reliably estimated, even when it is only 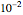 , either by ML or CGEMEV-ML. Concerning the starting point (here randomized) required by the iterative maximization of the likelihood, it may sometimes have a non-negligible impact; by changing the randomization seed from 321 to 1492, you can see a weak impact in this setting, even though the estimation of
, either by ML or CGEMEV-ML. Concerning the starting point (here randomized) required by the iterative maximization of the likelihood, it may sometimes have a non-negligible impact; by changing the randomization seed from 321 to 1492, you can see a weak impact in this setting, even though the estimation of  is now slightly worse than the one by CGEMEV-ML. However, if the iteration is stopped too early (try 50 instead of 100), the impact is strong; the seed 2018 greatly deteriorates the ML estimator of
is now slightly worse than the one by CGEMEV-ML. However, if the iteration is stopped too early (try 50 instead of 100), the impact is strong; the seed 2018 greatly deteriorates the ML estimator of 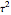 .
.
Snapshot 3: The meaning of "small  " in the previous statement depends on
" in the previous statement depends on  , as expected; here with
, as expected; here with 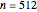 and
and 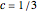 , the noise
, the noise 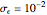 is still reliably estimated. This estimation is less accurate as
is still reliably estimated. This estimation is less accurate as  increases; this is the case already with
increases; this is the case already with 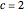 , even for ML where the upper bound
, even for ML where the upper bound  , imposed on the SNR, is often active, yet the estimation of the diffusion coefficient by
, imposed on the SNR, is often active, yet the estimation of the diffusion coefficient by 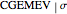 where
where  is arbitrarily set at
is arbitrarily set at 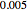 is still almost as efficient as ML in such a case.
is still almost as efficient as ML in such a case.
References
[1] D. A. Girard. "Estimating a Centered Ornstein–Uhlenbeck Process under Measurement Errors" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/EstimatingACenteredOrnsteinUhlenbeckProcessUnderMeasurementE.
[2] D. A. Girard, "Efficiently Estimating Some Common Geostatistical Models by ‘Energy–Variance Matching’ or Its Randomized ‘Conditional–Mean’ Versions," Spatial Statistics, 21(Part A), 2017 pp. 1–26. doi:10.1016/j.spasta.2017.01.001.
[3] M. Katzfuss and N. Cressie, "Bayesian Hierarchical Spatio‐temporal Smoothing for Very Large Datasets," Environmetrics, 23(1), 2012 pp. 94–107. doi:10.1002/env.1147.
[4] C. Gu, Smoothing Spline ANOVA Models, 2nd ed., New York: Springer, 2013.
[5] D. A. Girard. "Three Alternatives to the Likelihood Maximization for Estimating a Centered Matérn (3/2) Process" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/ThreeAlternativesToTheLikelihoodMaximizationForEstimatingACe.
[6] D. A. Girard. "Estimating a Centered Matérn (1) Process: Three Alternatives to Maximum Likelihood via Conjugate Gradient Linear Solvers" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/EstimatingACenteredMatern1ProcessThreeAlternativesToMaximumL.
[7] D. A. Girard. "Estimating a Centered Isotropic Matérn Field from a (Possibly Incomplete and Noisy) Lattice Observation." (Oct 1, 2018) github.com/didiergirard/CGEMEV.
[8] J. Staudenmayer and J.P. Buonaccorsi, "Measurement Error in Linear Autoregressive Models," Journal of the American Statistical Association, 100(471), 2005 pp. 841–852. doi.org/10.1198/016214504000001871.
Snapshots
Permanent Citation