Euclid's Construction of a Regular Icosahedron (XIII.16)

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
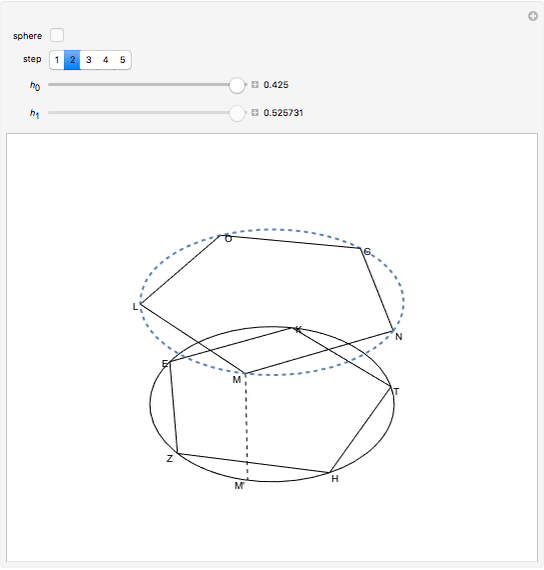
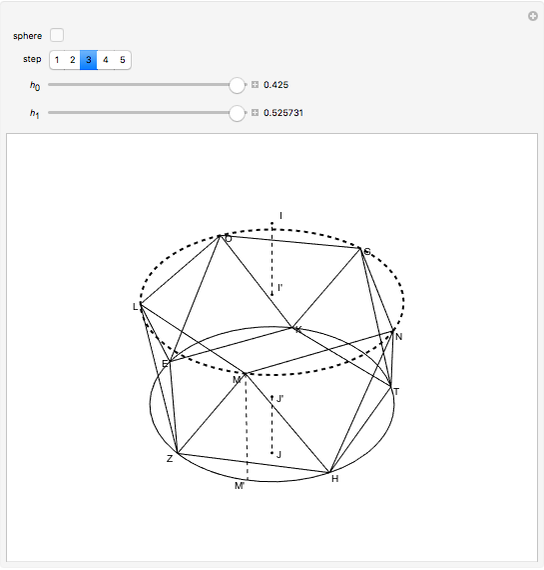
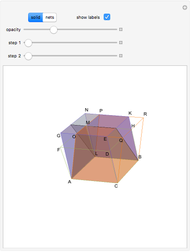
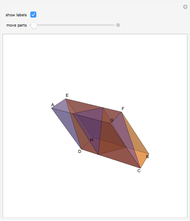
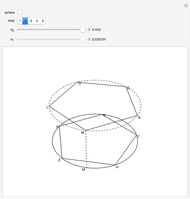
Let 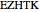 be a regular pentagon inscribed in circle
be a regular pentagon inscribed in circle  with radius
with radius  , and let
, and let  ,
, 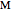 ,
,  ,
,  , and
, and 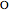 be the midpoints of the arcs
be the midpoints of the arcs 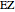 ,
, 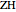 ,
, 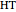 ,
, 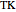 , and
, and 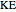 , respectively (step 2).
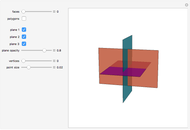
, respectively (step 2). 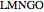 is also a regular pentagon. The slider
is also a regular pentagon. The slider 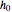 translates the pentagon
translates the pentagon 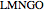 in the direction normal to its plane up to the length of the radius
in the direction normal to its plane up to the length of the radius  (
(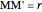 ). Let
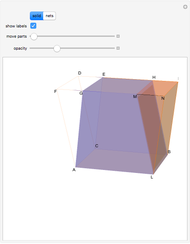
). Let 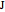 and
and  be the centers of
be the centers of 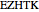 and
and 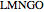 . The slider
. The slider 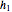 translates
translates  and
and 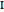 , also in the direction normal to the plane
, also in the direction normal to the plane  , to its maximum value, which is the length of a side of the regular decagon inscribed in circle
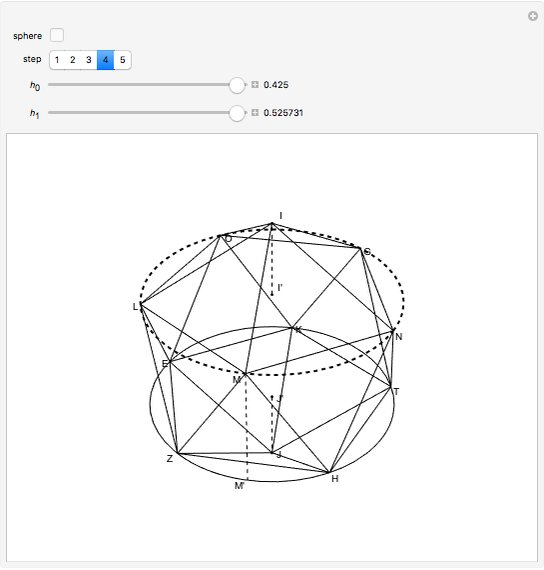
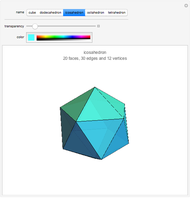
, to its maximum value, which is the length of a side of the regular decagon inscribed in circle  . The regular icosahedron is constructed by connecting corresponding points for maximum values of the sliders
. The regular icosahedron is constructed by connecting corresponding points for maximum values of the sliders 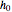 and
and 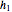 .
.
Contributed by: Milana Dabic (October 2011)
Open content licensed under CC BY-NC-SA
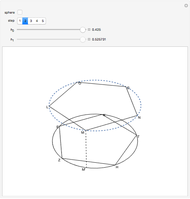
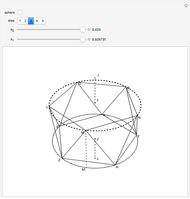
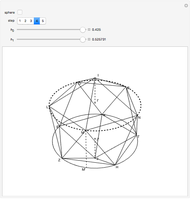
Snapshots
Details
detailSectionParagraphPermanent Citation
"Euclid's Construction of a Regular Icosahedron (XIII.16)"
http://demonstrations.wolfram.com/EuclidsConstructionOfARegularIcosahedronXIII16/
Wolfram Demonstrations Project
Published: October 19 2011