Euclid's Formula and Properties of Pythagorean Triples

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
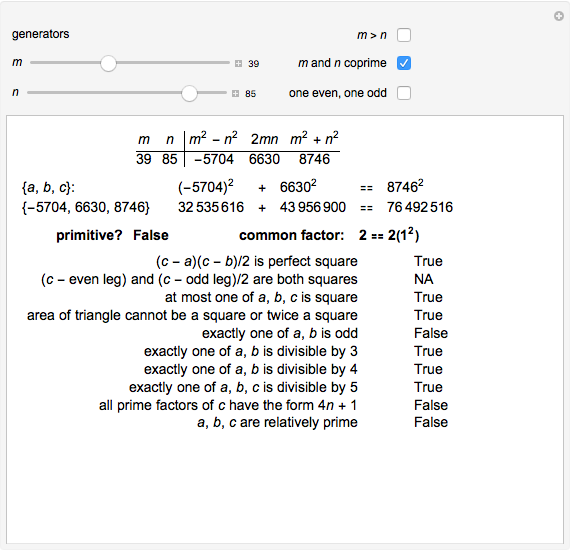
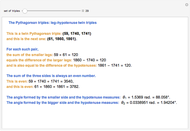
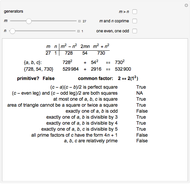
A Pythagorean triple consists of three integers  ,
,  and
and  , such that
, such that 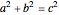 . If
. If  ,
,  and
and  are relatively prime, they form a primitive Pythagorean triple. Euclid’s formula generates a Pythagorean triple for every choice of positive integers
are relatively prime, they form a primitive Pythagorean triple. Euclid’s formula generates a Pythagorean triple for every choice of positive integers 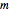 and
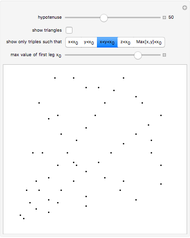
and  . Adjust the sliders to change the generating integers and see which of the tests are satisfied by the triple generated. Checkboxes apply additional restrictions.
. Adjust the sliders to change the generating integers and see which of the tests are satisfied by the triple generated. Checkboxes apply additional restrictions.
Contributed by: Kenneth E. Caviness and R. Lewis Caviness (March 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
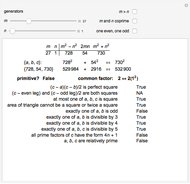
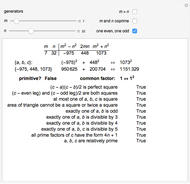
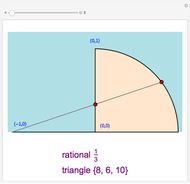
This Demonstration lets you experiment with the properties of Pythagorean triples (PTs). A PT gives the lengths of the sides of a right triangle. For example, both 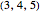 and
and 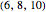 are PTs, since they satisfy the equation
are PTs, since they satisfy the equation 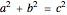 . The second triple is not primitive, because the sides have a common factor of 2, which could be divided out.
. The second triple is not primitive, because the sides have a common factor of 2, which could be divided out.
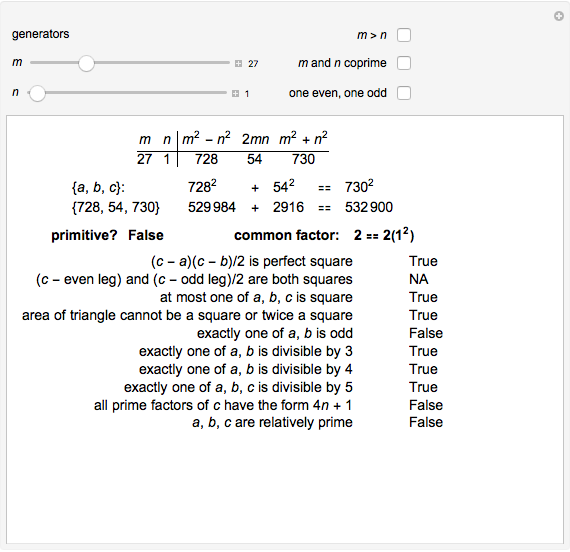
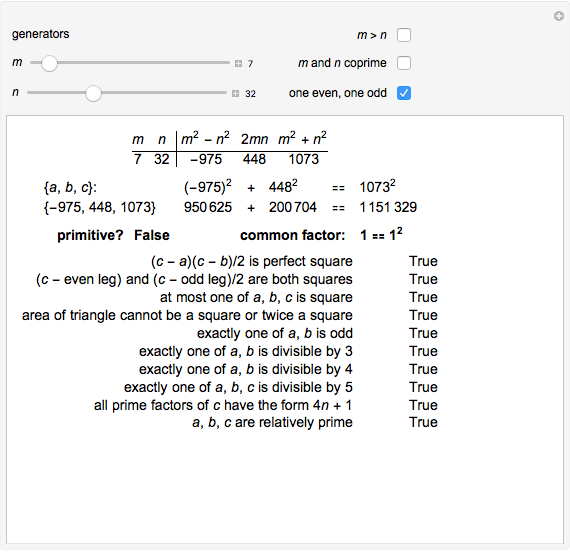
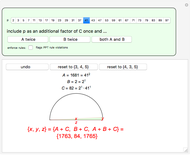
Euclid’s formula is 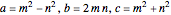 . It gives a PT for every choice of positive integers
. It gives a PT for every choice of positive integers 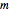 and
and  .
.
A series of tests is marked "True" or "False" for the PT generated: some are true for all PTs, others only for primitive Pythagorean triples (PPTs).
You can check boxes to restrict the generating integers 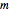 and
and  ; a particular choice of these entirely eliminates the nonprimitive cases generated.
; a particular choice of these entirely eliminates the nonprimitive cases generated.
It is not hard to show algebraically why Euclid’s formula holds, and it is interesting to note that although the formula generates all PPTs, it does not give all PTs, even when the additional restrictions are lifted. The common factors are shown so that you can experiment to find the form of the non-PPTs that arise.
Permanent Citation