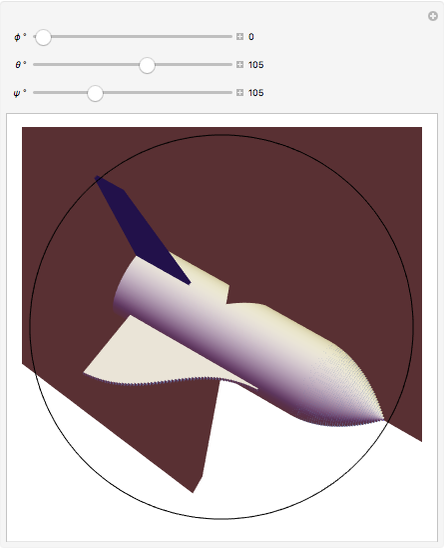
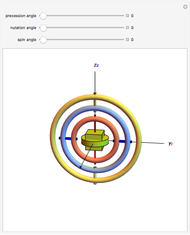
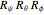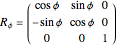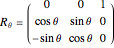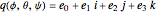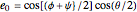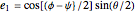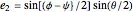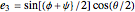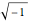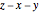Euler Angles for Space Shuttle

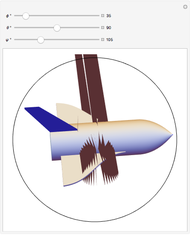
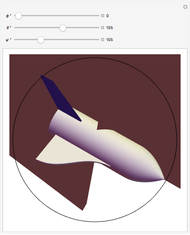
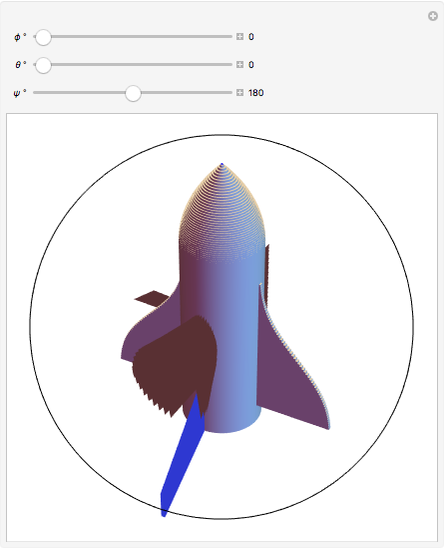
The Euler (or Eulerian) angles, usually designated , , and , uniquely determine the orientation of a rigid body in three-dimensional space. There are several conflicting conventions for defining the Euler angles, depending on the choice of axes and the order in which rotations about these axes are performed. This Demonstration uses the convention described in MathWorld, hyperlinked below in Related Links. This is most commonly used in physics and is known as the "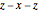 convention." For topical relevance, NASA's space shuttle is chosen as the rigid body. The angles and are analogous to the spherical polar coordinates orienting the main axis of the shuttle, while describes rotation about this axis. The ranges of the three Euler angles are given by: 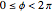, , 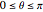and . The corresponding motions of a rigid body are termed nutation, precession and intrinsic rotation.

Any rotation of a rigid body can be represented as the product of three successive rotations , with matrix representations

, , .

A unit vector with Euler angles , , and can also be represented by a quaternion , where

, , , ,

and successive rotations obey the algebra of quaternion multiplication. The same combination rule pertains to a linear combination of Pauli spin matrices: , where is the 2×2 unit matrix and means .

In aeronautic or astronautic applications, the " convention" is most often used. The angles , , and are then known as Tait-Bryan rotations, called pitch, yaw, and roll, respectively.