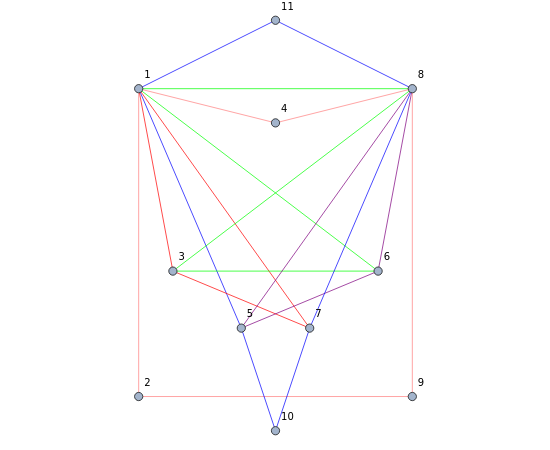
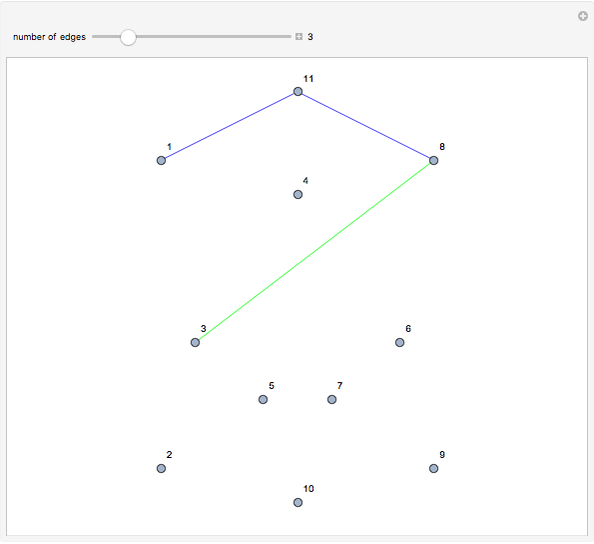
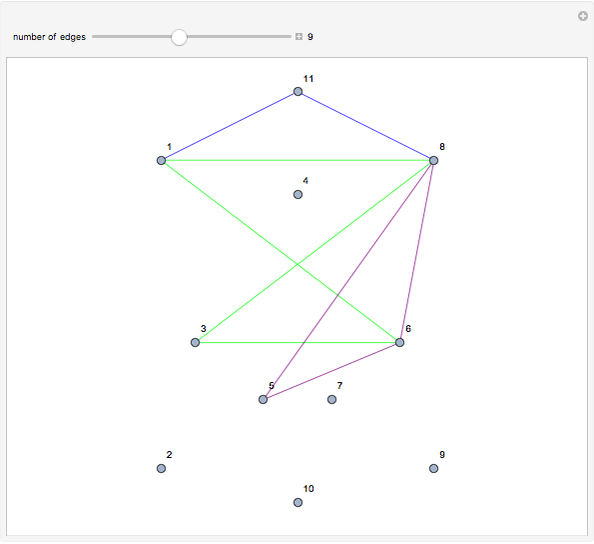
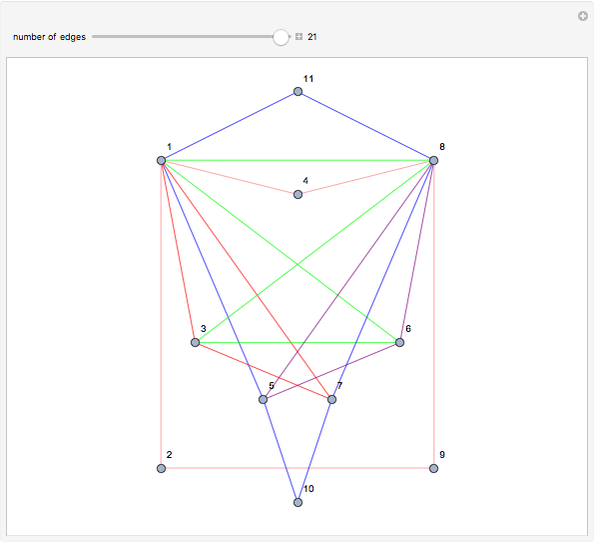
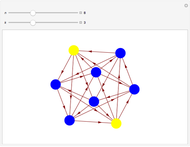
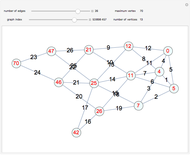
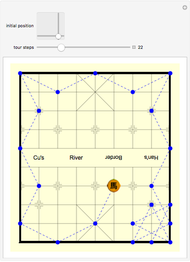
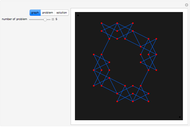
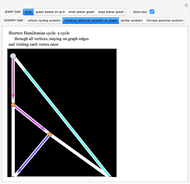
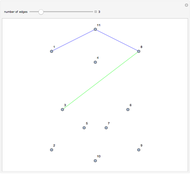
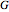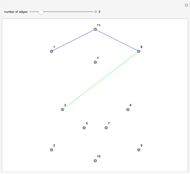
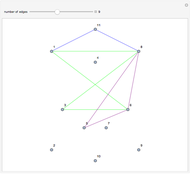
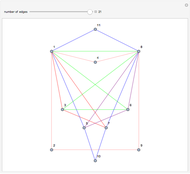
This Demonstration shows an example of a well-known result in graph theory that states that a connected graph is Eulerian iff it has a cycle decomposition, that is, a family of edge-disjoint cycles whose union is 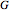. As you drag the slider, you see an Eulerian path that travels the edges of the decomposition and colors each edge of the graph with a color corresponding to the cycle of the decomposition containing the edge. With the maximum number of edges, you can clearly see the complete cycle decomposition of the graph.