Euler's Polyhedral Formula

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
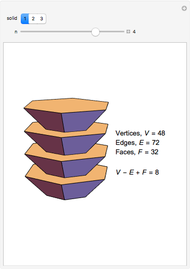
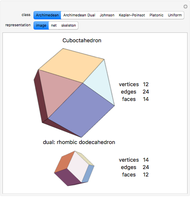
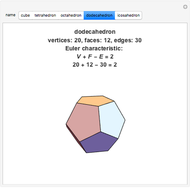
Let the number of vertices, edges, and faces of a polyhedron be  ,
,  , and
, and  . The Euler characteristic,
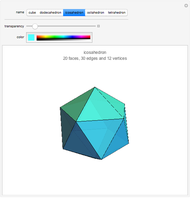
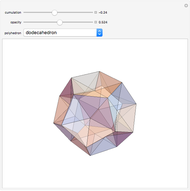
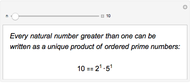
. The Euler characteristic,  , is always 2 for convex polyhedra. This Demonstration shows Euler's polyhedral formula
, is always 2 for convex polyhedra. This Demonstration shows Euler's polyhedral formula  for the Platonic solids.
for the Platonic solids.
Contributed by: Hector Zenil (September 2007)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Euler's Polyhedral Formula"
http://demonstrations.wolfram.com/EulersPolyhedralFormula/
Wolfram Demonstrations Project
Published: September 28 2007