Evolution of a Gaussian Wave Packet

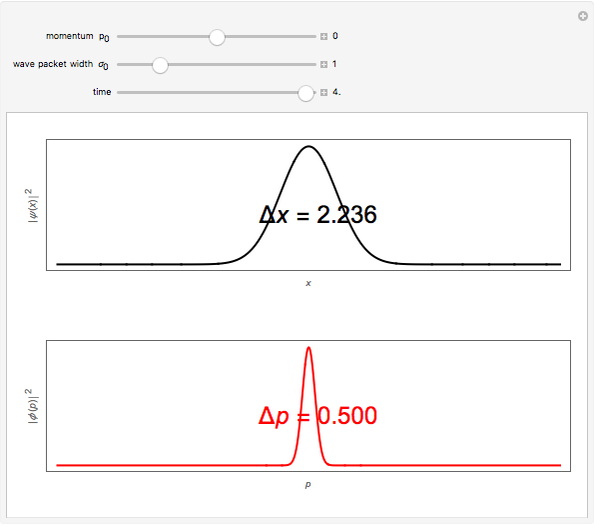
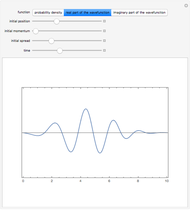
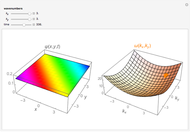
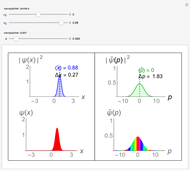
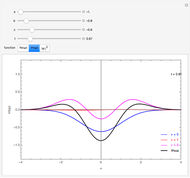
A Gaussian wave packet centered around at time with an average initial momentum can be represented by the wavefunction . (For convenience, we take .) The solution of the free-particle Schrödinger equation with this initial condition works out to . The probability density is then given by , where , shown as a black curve. The wave packet remains Gaussian as it spreads out, with its center moving to , thereby following the classical trajectory of the particle. The corresponding momentum probability distribution is given by , shown in red. The rms uncertainties are given by , , which is independent of . This is consistent with the fact that is a constant of the motion for a free particle.

Thus, with ℏ put back in, the uncertainty product is given by , in accord with Heisenberg's uncertainty principle. At , the Gaussian probability distribution represents a minimum uncertainty wave packet with , but the product increases when .

In this Demonstration, you can drag the time slider to simulate the simultaneous time evolution of the probability and momentum distributions. Note that the distribution broadens with time while the distribution maintains its original width. The numerical values of , , and are illustrative only and have no absolute significance.