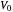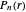Exact Solutions of the Schrödinger Equation for Pseudoharmonic Potential

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
The pseudoharmonic potential  belongs to the small number of problems for which the Schrödinger equation is exactly solvable [1] and is thus of intrinsic interest. The solution is outlined in the Details below.
belongs to the small number of problems for which the Schrödinger equation is exactly solvable [1] and is thus of intrinsic interest. The solution is outlined in the Details below.
Contributed by: S. M. Blinder (May 2019)
Open content licensed under CC BY-NC-SA
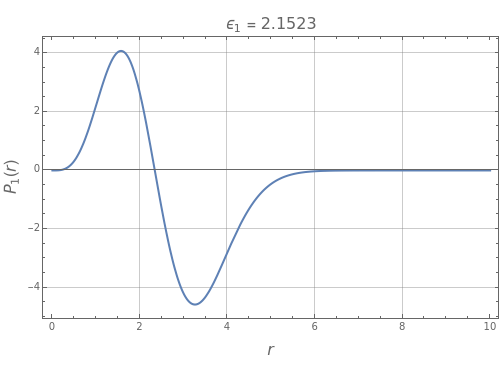
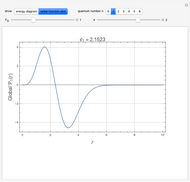
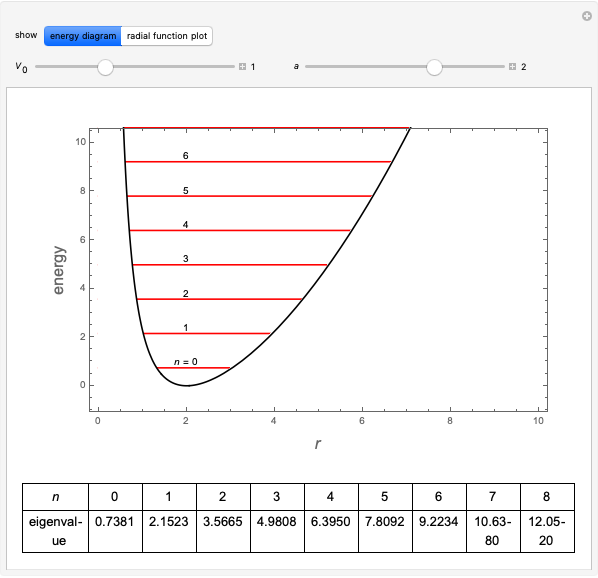
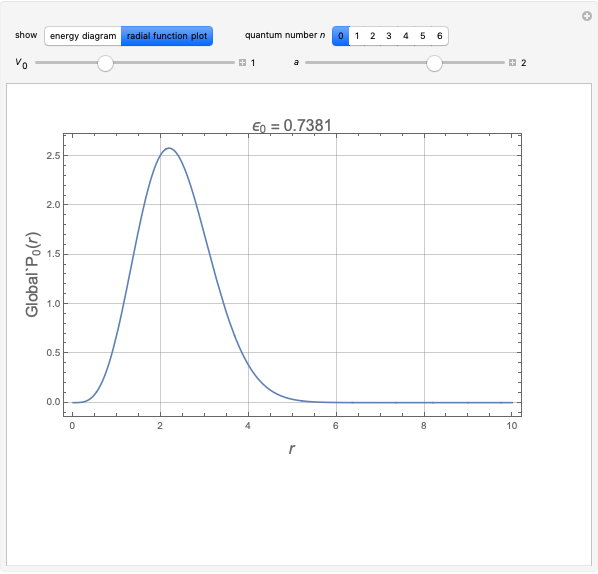
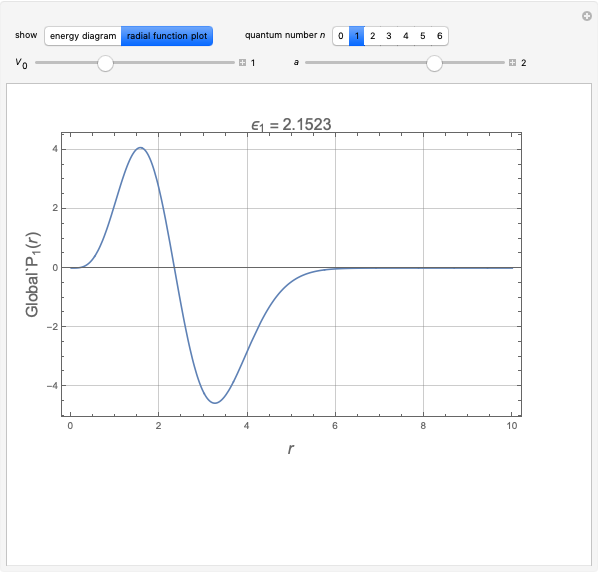
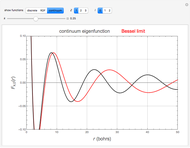
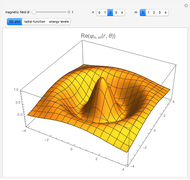
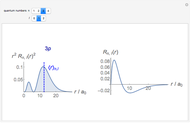
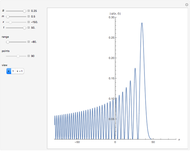
Snapshots
Details
The Schrödinger equation for the radial function 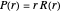 , in the case of zero angular momentum, is given by
, in the case of zero angular momentum, is given by
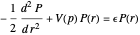 .
.
The eigenfunctions for bound states are found to be
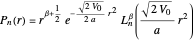 ,
,
where  is an associated Laguerre polynomial. The solution of the differential equation initially gave associated Laguerre functions
is an associated Laguerre polynomial. The solution of the differential equation initially gave associated Laguerre functions  , with
, with

and
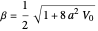 .
.
The quantization is determined by the condition that the eigenfunctions must approach 0 as 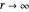 . The asymptotic behavior of Laguerre functions is given by:
. The asymptotic behavior of Laguerre functions is given by:

as 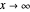 .
.
This would overtake the converging factor  in the solution as
in the solution as  , unless
, unless 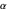 is an integer
is an integer  , which would then produce a singularity in a gamma function of the denominator. The corresponding eigenvalues are thereby determined:
, which would then produce a singularity in a gamma function of the denominator. The corresponding eigenvalues are thereby determined:

with 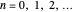 .
.
Reference
[1] I. I. Gol'dman and V. D. Krivchenkov, Problems in Quantum Mechanics (B. T. Ge\:01d0likman, ed., E. Marquit and E. Lepa, trans.), Reading, MA: Addison-Wesley, 1961.\:202c
Permanent Citation