Exit Times of Brownian Motion in 3D

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
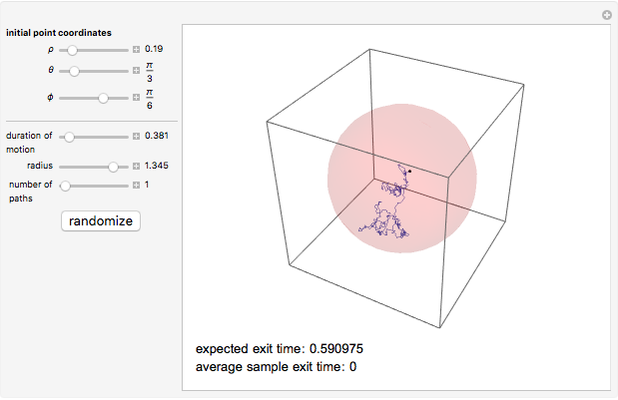
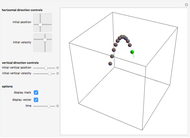
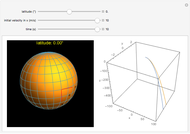
The expected first exit time of a particle in Brownian motion starting from a point with position vector  from a ball of radius
from a ball of radius 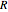 in
in  dimensions is
dimensions is 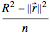 . We demonstrate this for
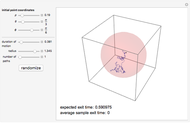
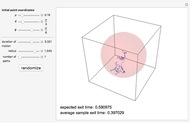
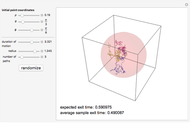
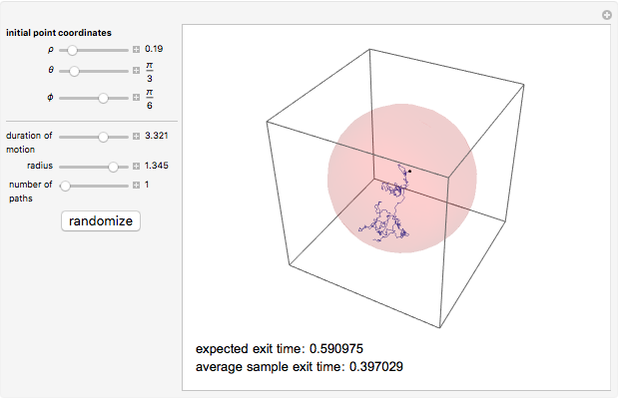
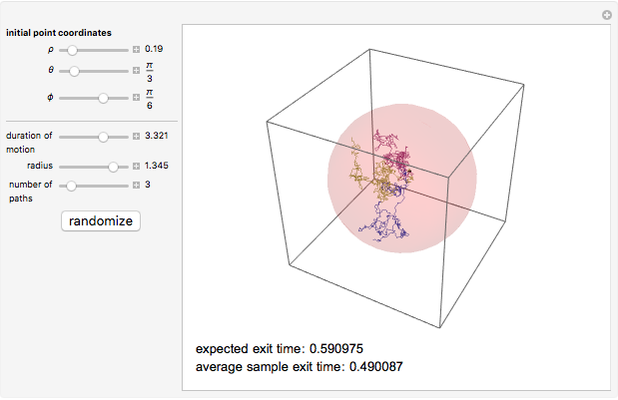
. We demonstrate this for 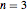 . Choose the radius of the ball, the position of the initial point, and the number of paths; vary the duration of motion until all the paths hit the boundary. The expected exit time and the average of the exit times for the particular sample generated are displayed in the lower left corner. Once a Brownian path hits the boundary, it no longer changes and further increasing the duration of motion has no effect.
. Choose the radius of the ball, the position of the initial point, and the number of paths; vary the duration of motion until all the paths hit the boundary. The expected exit time and the average of the exit times for the particular sample generated are displayed in the lower left corner. Once a Brownian path hits the boundary, it no longer changes and further increasing the duration of motion has no effect.
Contributed by: Andrzej Kozlowski (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The formula for the expected first exit time can be easily deduced from the well-known formula of Dynkin for the expected value of a 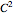 -function in
-function in  at a finite stopping time (see B. K. Øksendal, Stochastic Differential Equations, pp. 120–122). It is interesting to note that when the starting point is taken outside the disk, there is a startling difference between the cases
at a finite stopping time (see B. K. Øksendal, Stochastic Differential Equations, pp. 120–122). It is interesting to note that when the starting point is taken outside the disk, there is a startling difference between the cases 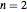 and
and 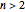 . In the former the Brownian path eventually enters the disk with probability 1; in the latter the expected entry time is infinite. In the Demonstration one can choose the initial point outside the ball, but, of course, in this case no conclusions about the expected entrance time can be drawn from the simulation.
. In the former the Brownian path eventually enters the disk with probability 1; in the latter the expected entry time is infinite. In the Demonstration one can choose the initial point outside the ball, but, of course, in this case no conclusions about the expected entrance time can be drawn from the simulation.
Permanent Citation