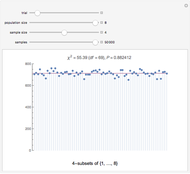
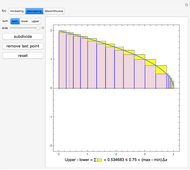
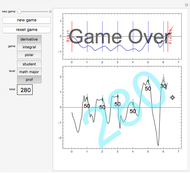
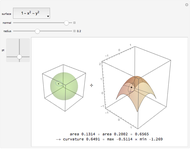
Expansion and Divergence

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
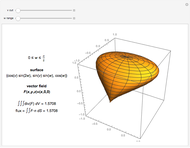
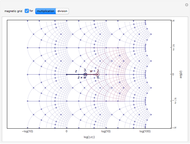
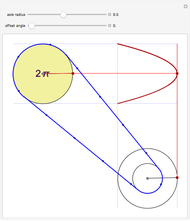
Imagine a moving fluid that may possibly expand or contract, such as a gas. Each point has a velocity vector, making all the points into what is called a vector field. At each point in the flow, the divergence of a vector field indicates the relative rate of expansion of the flow. The divergence can be visualized as follows. Near a selected point, let there be a given small cubical volume containing the point. As time changes, the volume will change shape and magnitude. The relative change in volume 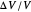 will be roughly proportional to the divergence of the vector field and the amount of time elapsed. Indeed, the divergence is equal to the limit of
will be roughly proportional to the divergence of the vector field and the amount of time elapsed. Indeed, the divergence is equal to the limit of 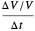 as the change in time
as the change in time 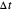 approaches zero.
approaches zero.
Contributed by: Michael Rogers (August 2010)
(Oxford College of Emory University)
Open content licensed under CC BY-NC-SA
Snapshots
Details
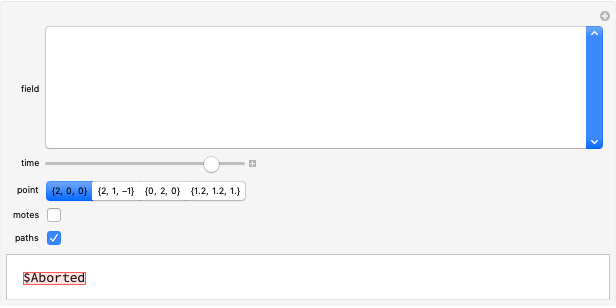
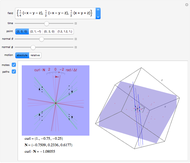
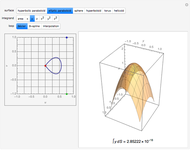
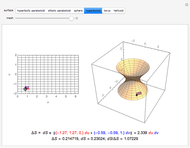
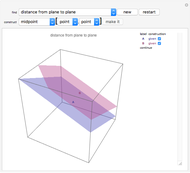
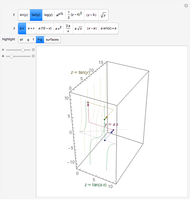
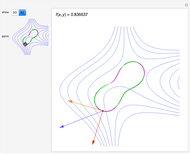
Select a vector field and one of the points to study. Use the slider for the time to animate the volume. For reference, a coordinate trihedron is drawn at the origin. The initial cubical volume 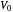 is drawn in blue; the volume
is drawn in blue; the volume 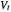 at the current time is drawn in red. A numerical comparison of the rate of change in volume and the divergence is given in the lower left. The blue paths, which show the paths of the corners of the volume, and the motes, which help show the overall flow, may be switched on or off.
at the current time is drawn in red. A numerical comparison of the rate of change in volume and the divergence is given in the lower left. The blue paths, which show the paths of the corners of the volume, and the motes, which help show the overall flow, may be switched on or off.
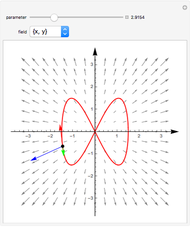
The vector fields: The first six vector fields are linear. They have a constant divergence, although the flow can look different at different points. The first three, 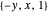 ,
, 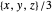 , and
, and 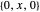 , are basic, linear fields: (1) the composition of a rotation about the
, are basic, linear fields: (1) the composition of a rotation about the  axis and a translation along the
axis and a translation along the  axis, (2) an expansion, and (3) a shear motion. The next three,
axis, (2) an expansion, and (3) a shear motion. The next three, 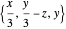 ,
, 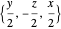 , and
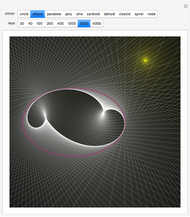
, and 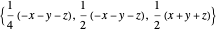 , are slightly more complicated linear fields. The last four vector fields are nonlinear. The first,
, are slightly more complicated linear fields. The last four vector fields are nonlinear. The first, 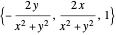 , is incompressible (the divergence is zero throughout its domain) and has swirling, helical flow paths. The last three,
, is incompressible (the divergence is zero throughout its domain) and has swirling, helical flow paths. The last three, 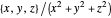 ,
, 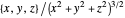 , and
, and 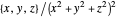 , like the second, linear one, expand from the origin. These illustrate how flow paths might expand and the divergence of the vector field is positive, zero, or negative, respectively. The last three fields also approach a singularity in finite time. The domain is restricted in these cases and the time slider has no effect outside the domain.
, like the second, linear one, expand from the origin. These illustrate how flow paths might expand and the divergence of the vector field is positive, zero, or negative, respectively. The last three fields also approach a singularity in finite time. The domain is restricted in these cases and the time slider has no effect outside the domain.
A note on the difference between the instantaneous divergence and the average rate of change of the volume over a finite time: For linear fields the cubical volume remains a parallelepiped throughout time. Its volume 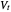 can be computed exactly. Since the relative growth rate of the volume, which is equal to the divergence, is constant, the volume grows exponentially, except for incompressible fields, which have a divergence of zero. For nonlinear fields, the volume deforms and its magnitude
can be computed exactly. Since the relative growth rate of the volume, which is equal to the divergence, is constant, the volume grows exponentially, except for incompressible fields, which have a divergence of zero. For nonlinear fields, the volume deforms and its magnitude 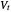 is estimated only approximately. In both the linear and nonlinear cases, the average rate approaches the divergence as the change in time approaches zero, just as in introductory calculus the slope of the secant line approaches the tangent line as the change in
is estimated only approximately. In both the linear and nonlinear cases, the average rate approaches the divergence as the change in time approaches zero, just as in introductory calculus the slope of the secant line approaches the tangent line as the change in 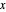 approaches zero.
approaches zero.
Permanent Citation