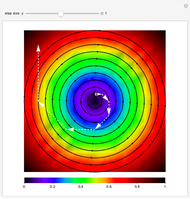
Expected Dynamics of an Imitation Model in 2x2 Symmetric Games
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
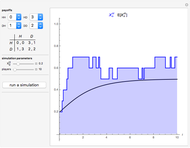
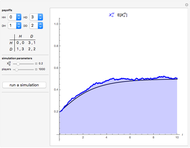
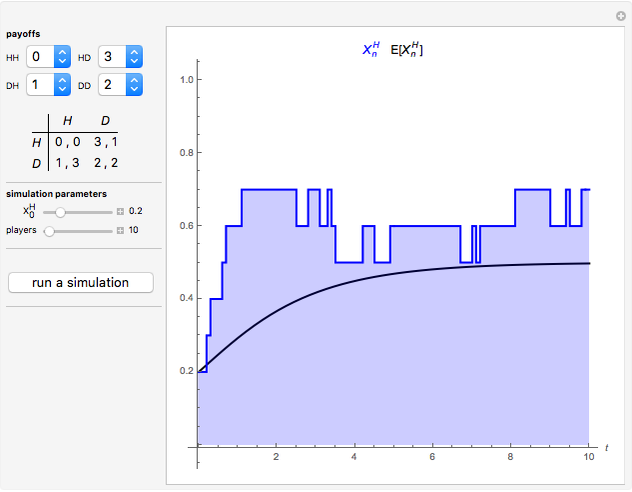
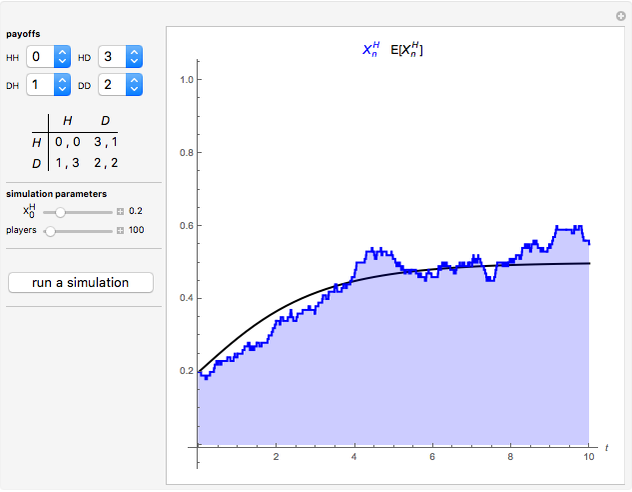
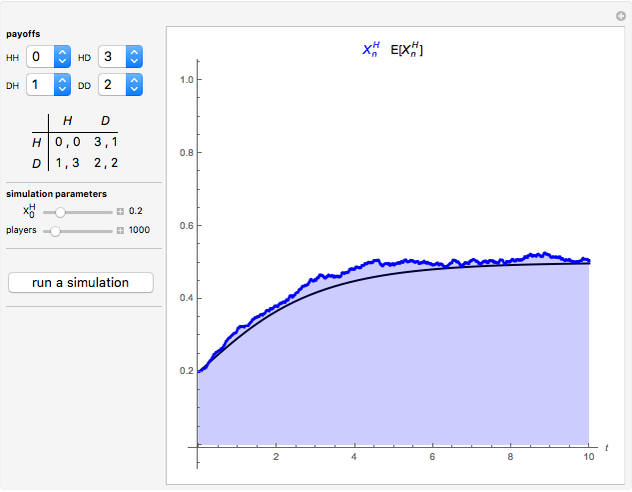
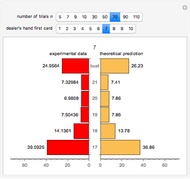
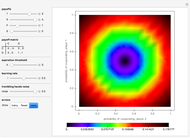
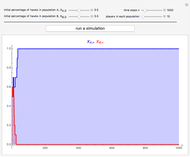
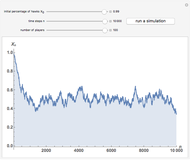
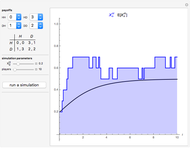
The figure shows the actual (in blue) and expected (in black) proportion of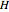 
-strategists in a population of 
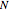individuals who, at each iteration (of time length 
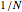), are randomly matched in pairs to play a symmetric 2×2 game. The two possible actions (or pure strategies) in the game are labeled 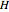and 
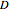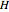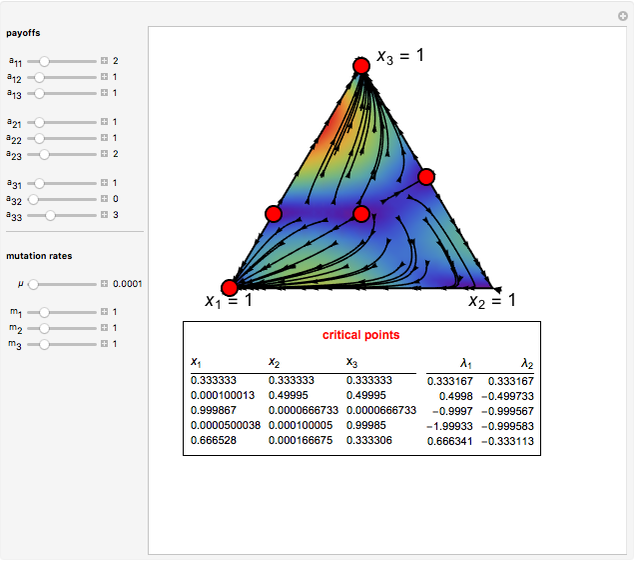
. Thus, each individual in the population is either an -strategist or a 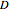-strategist. The payoffs of the game are 
, 
, 
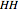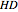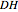, and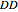 
(parameters), where, for instance, 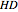denotes the payoff obtained by an 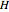-strategist when he plays with a 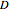-strategist.
Contributed by: Luis R. Izquierdo and Segismundo S. Izquierdo (May 2010)
Open content licensed under CC BY-NC-SA
Snapshots
Details
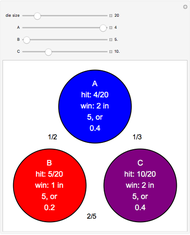
The first three Snapshots show the Hawk-Dove game in a population of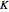 
individuals ( 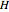denotes the Hawk strategy and 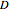denotes the Dove strategy).
Snapshot 1: 
Snapshot 2: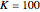 
Snapshot 3: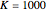 
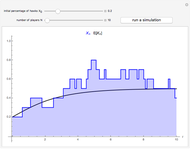
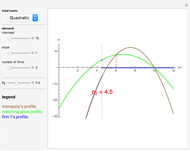
The last three Snapshots show the Prisoner's Dilemma game in a population of 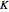individuals ( 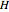denotes the cooperative strategy and 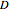denotes the defective strategy).
Snapshot 4:
Snapshot 5: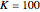
Snapshot 6: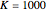
Reference
[1] S. S. Izquierdo and L. R. Izquierdo, "Stochastic Approximation to Understand Simple Simulation Models," Journal of Statistical Physics, Dec 2012. dx.doi.org/10.1007/s10955-012-0654-z. Download preprint.
Permanent Citation
Expected Dynamics of an Intra-Population Imitation Model for Inter-Population 2x2 Symmetric Games
Luis R. Izquierdo and Segismundo S. Izquierdo
An Imitation Model for 2x2 Symmetric Games
Luis R. Izquierdo and Segismundo S. Izquierdo
An Intra-Population Imitation Model for Inter-Population 2x2 Symmetric Games
Luis R. Izquierdo and Segismundo S. Izquierdo
Expected Dynamics of an Imitation Model in the Hawk-Dove Game
Luis R. Izquierdo and Segismundo S. Izquierdo
Dealer's Odds in Blackjack
D. Meliga and S. Z. Lavagnino
Expected Motion in 2x2 Symmetric Games Played by Reinforcement Learners
Luis R. Izquierdo and Segismundo S. Izquierdo
Truel World
Ed Pegg Jr
Bertrand Competition with Linear or Quadratic Costs
Massimiliano Landi
Expected Dynamics of an Intra-Population Imitation Model in the Two-Population Hawk-Dove Game
Luis R. Izquierdo and Segismundo S. Izquierdo
Throwing a Die to Score 100 Points
Heikki Ruskeepää
-
Mixing and Infection in a Two-Group SIS Model
Segismundo S. Izquierdo -
Expected Dynamics of an Intra-Population Imitation Model in the Two-Population Hawk-Dove Game
Segismundo S. Izquierdo -
An Intra-Population Imitation Model in the Two-Population Hawk-Dove Game
Segismundo S. Izquierdo -
Expected Dynamics of an Imitation Model in the Hawk-Dove Game
Segismundo S. Izquierdo -
An Imitation Model in the Hawk-Dove Game
Segismundo S. Izquierdo -
Expected Motion in 2x2 Symmetric Games Played by Reinforcement Learners
Segismundo S. Izquierdo -
Expected Dynamics of an Imitation Model in 2x2 Symmetric Games
Segismundo S. Izquierdo -
An Intra-Population Imitation Model for Inter-Population 2x2 Symmetric Games
Segismundo S. Izquierdo -
Inference with Fuzzy IF-THEN Rules
Segismundo S. Izquierdo -
An Imitation Model for 2x2 Symmetric Games
Segismundo S. Izquierdo -
Expected Dynamics of an Intra-Population Imitation Model for Inter-Population 2x2 Symmetric Games
Segismundo S. Izquierdo -
Replicator-Mutator Dynamics with Three Strategies
Segismundo S. Izquierdo -
Difference Equation versus Differential Equation
Segismundo S. Izquierdo