Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Exponential Congruences

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

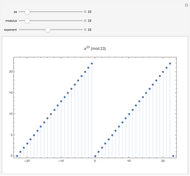
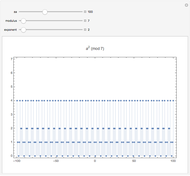
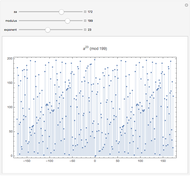
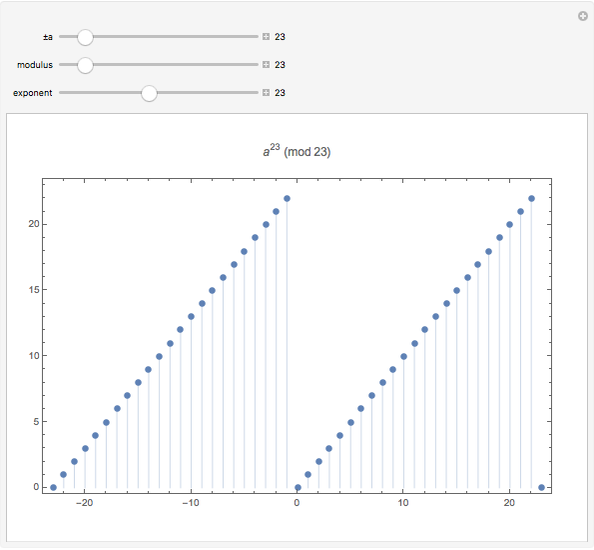
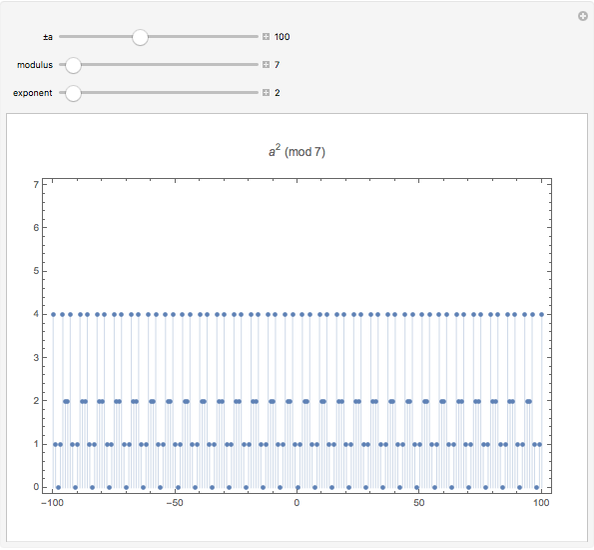
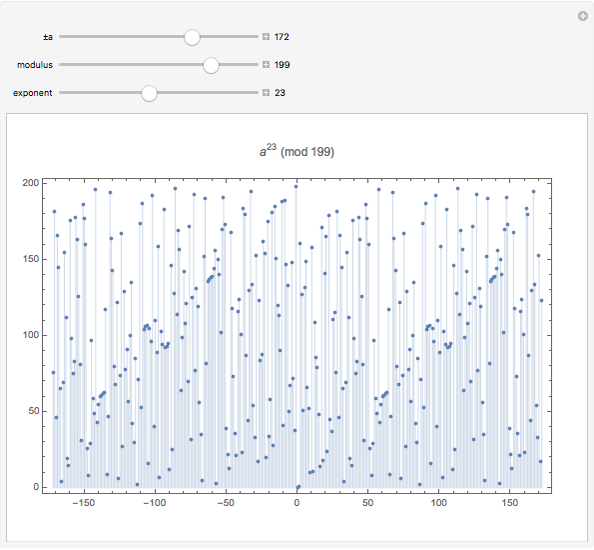
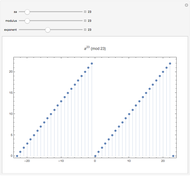
Congruences of the form 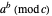display many regular patterns, as explained by theorems from Fermat and Euler, among others. The plot shows the values of 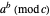within the complete residue system 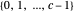for domain values 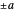, the modulus , and the exponent .

Contributed by: Richard Roe (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

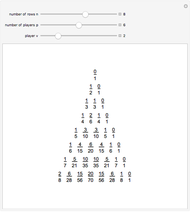
Snapshot 1: little Fermat theorem

Snapshot 2: quadratic residues of 7

The initial settings are a particular demonstration of Euler's criterion.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send