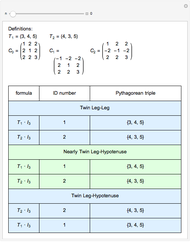
Extended Euclidean Algorithm

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
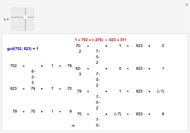
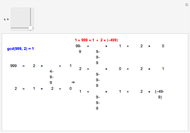
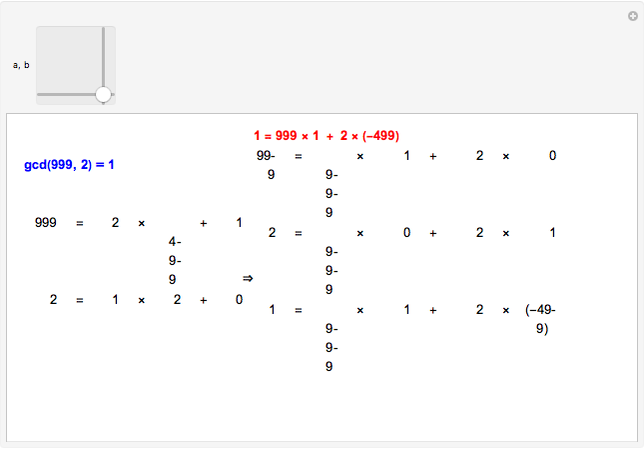
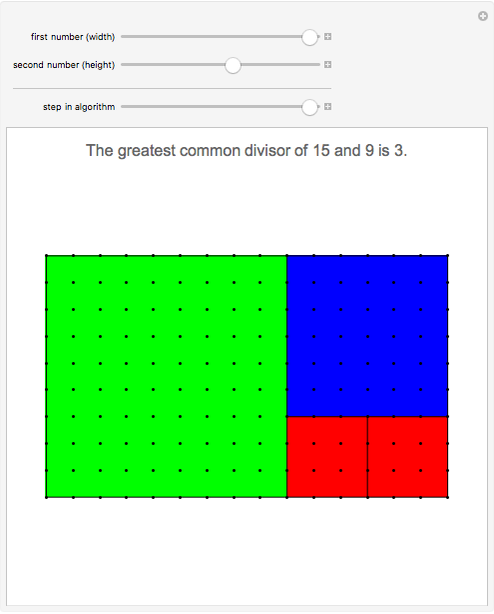
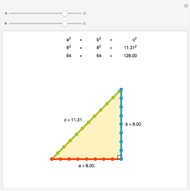
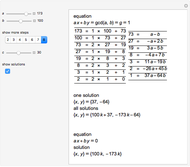
The greatest common divisor of two integers 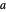 and
and  can be found by the Euclidean algorithm by successive repeated application of the division algorithm. The extended Euclidean algorithm not only computes
can be found by the Euclidean algorithm by successive repeated application of the division algorithm. The extended Euclidean algorithm not only computes 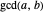 but also returns the numbers
but also returns the numbers  and
and  such that
such that  . The remainder
. The remainder 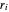 of the
of the  step in the Euclidean algorithm can be expressed in the form
step in the Euclidean algorithm can be expressed in the form 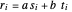 , where
, where 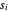 and
and 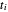 can be determined from the corresponding quotient
can be determined from the corresponding quotient  and the values
and the values 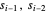 , or
, or 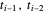 two rows above them using the relations
two rows above them using the relations 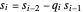 and
and 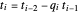 , respectively. This forward method requires no back substitutions and reduces the amount of computation involved in finding the coefficients
, respectively. This forward method requires no back substitutions and reduces the amount of computation involved in finding the coefficients  and
and  of the linear combination.
of the linear combination.
Contributed by: Štefan Porubský (March 2011)
Based on a program by: Michael Trott
Open content licensed under CC BY-NC-SA
Snapshots
Details
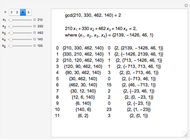
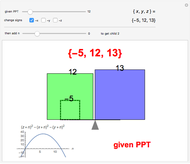
The result saying that the greatest common divisor of any two integers  and
and  can be written as their linear combination is also known as the Bachet–Bézout theorem (actually, Bézout formulated it for polynomials).
can be written as their linear combination is also known as the Bachet–Bézout theorem (actually, Bézout formulated it for polynomials).
For more information, see the Wikipedia entry for Extended Euclidean algorithm.
The underlying Mathematica code is an adaptation of the code used in the Demonstration Euclidean Algorithm Steps by Michael Trott.
(The author was supported by project 1ET200300529 of the Information Society of the National Research Program of the Czech Republic and by the Institutional Research Plan AV0Z10300504; the Demonstration was submitted 2008-06-20, revised 2010-03-13.)
Permanent Citation